Question

8．如图1，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，

（1）若∠1=40°，∠2=30°，求∠A的度数；
（2）通过第（1）请你写出∠1、∠2与∠A的关系∠1+∠2=2∠A；
（3）把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外部如图2所示时，请你直接写出∠1、∠2与∠A的关系∠A=$\frac{1}{2}$（∠1-∠2）．．

Answer 1

分析 （1）连接AA′，根据折叠的性质得到∠DAE=∠DA′E，根据三角形的外角的性质计算即可；
（2）与（1）的证明过程类似，证明即可；
（3）根据折叠的性质和三角形内角和定理解答即可．

解答 解：（1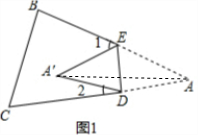）如图1，连接AA′．
则△A′ED即为折叠前的三角形，
由折叠的性质知：∠DAE=∠DA′E．
由三角形的外角性质知：
∠1=∠EAA′+∠EA′A，∠2=∠DAA′+∠DA′A；
则∠1+∠2=∠DAE+∠DA′E=2∠DAE，
即∠1+∠2=2∠A，
则∠A=35°；
（2）连接AA′．
则△A′ED即为折叠前的三角形，
由折叠的性质知：∠DAE=∠DA′E．
由三角形的外角性质知：
∠1=∠EAA′+∠EA′A，∠2=∠DAA′+∠DA′A；
则∠1+∠2=∠DAE+∠DA′E=2∠DAE，
即∠1+∠2=2∠A，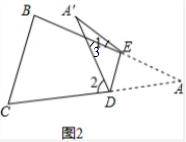
故答案是：∠1+∠2=2∠A；
（3）∵△A′DE是△ADE沿DE折叠得到，
∴∠A′=∠A，
又∵∠AEA′=180°-∠2，∠3=∠A′+∠1，
∴∠A+∠AEA′+∠3=180°，
即∠A+180°-∠2+∠A′+∠1=180°，
整理得，2∠A=∠2-∠1．
∴∠A=$\frac{1}{2}$（∠1-∠2）．
故答案为：∠A=$\frac{1}{2}$（∠1-∠2）．

点评 本题考查的是三角形的外角性质和图形的翻折变换，理清图中角与角的关系是解决问题的关键．