题目内容
16. 阅读材料:
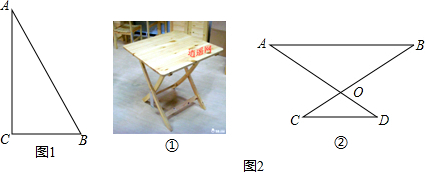
阅读材料:我们曾经解决过如下问题:“如图,点M,N分别在直线AB同侧,如何在直线AB上找到一个点P,使得PM+PN最小?”
我们可以经过如下步骤解决这个问题:
(1)画草图(或目标图)分析思路:在直线AB上任取一点P′,连接P′M,P′N,根据题目需要,作点M关于直线AB的对称点M′,将P′M+P′N转化为P′M′+P′N′,“化曲为直”寻找P′M′+P′N的最小值;
(2)设计画图步骤;
(3)回答结论并验证.
借鉴阅读材料中解决问题的三个步骤完成以下尺规作图:
已知三条线段h,m,c,求作△ABC,使其BC边上的高AH=h,中线AD=m,AB=c.

(1)请先画草图(画出一个即可),并叙述简要的作图思路(即实现目标图的大致作图步骤);
(2)完成尺规作图(不要求写作法,作出一个满足条件的三角形即可).
分析 (1)根据BC边上的高AH=h,中线AD=m,AB=c进行作图即可;
(2)先由长为h,m的两条线段作Rt△ADH,再由线段c作边AB确定点B,再倍长BD确定点C即可.
解答 解:(1)草图如图所示:
作图思路:先由长为h,m的两条线段作Rt△ADH,再由线段c作边AB确定点B,再倍长BD确定点C.
(2)如图所示,△ABC即为所求.
点评 本题主要考查了运用轴对称变换进行作图,解决问题的关键是先作出Rt△ADH.解题时时注意:解决此类题目需要熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
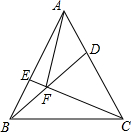 如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.
如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.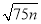 是整数,则正整数n的最小值是( )
是整数,则正整数n的最小值是( ) 如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标