题目内容
5.阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即:a2±2ab+b2=(a±b)2.根据阅读材料解决下面问题:
(1)m2+4m+4=(m+2)2
(2)无论n取何值,9n2-6n+1≥0(填“<”,“>”,“≤”,“≥”或“=”)
(3)已知m,n是△ABC的两条边,且满足10m2+4n2+4=12mn+4m,若该三角形的第三边k的长是奇数,求k的长.
分析 (1)根据完全平方式得出结论;
(2)9n2-6n+1=(3n-1)2≥0;
(3)将已知等式配方后,利用非负性得结论:$\left\{\begin{array}{l}{3m-2n=0}\\{m-2=0}\end{array}\right.$,求出m和n的值,再根据三角形的三边关系得出k的值.
解答 解:(1)原式=(m+2)2;
故答案为:m+2;
(2)9n2-6n+1=(3n-1)2≥0;
∴无论n取何值,9n2-6n+1≥0,
故答案为:≥;
(3)10m2+4n2+4=12mn+4m,
已知等式整理得:9m2-12mn+4n2+m2-4m+4=0,
(3m-2n)2+(m-2)2=0,
$\left\{\begin{array}{l}{3m-2n=0}\\{m-2=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$,
∵m,n是△ABC的两条边,
∴3-2<k<3+2,
1<k<5,
∵第三边k的长是奇数,
∴k=3.
点评 本题考查了完全平方式,正确读懂题目中的阅读材料,理解配方的方法和熟练掌握完全平方公式是关键.另外,注意分组的技巧和方法.

练习册系列答案
相关题目
18.若a、b互为相反数,则a+b-(-2)的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | ±2 |
10.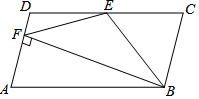 如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足F在线段AD上,连接EF.则下列结论一定成立的是( )
如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足F在线段AD上,连接EF.则下列结论一定成立的是( )
①∠FBC=90°;②点E是CD中点;③EF=EB;④S△EBF=S△EDF+S△EBC.
 如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足F在线段AD上,连接EF.则下列结论一定成立的是( )
如图,在平行四边形ABCD中,AB=2AD,BE平分∠ABC交CD于点E,作BF⊥AD,垂足F在线段AD上,连接EF.则下列结论一定成立的是( )①∠FBC=90°;②点E是CD中点;③EF=EB;④S△EBF=S△EDF+S△EBC.
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②③④ |
17.计算2×(-3)2的结果是( )
| A. | -12 | B. | 12 | C. | 18 | D. | 36 |
14.下列各组数为三角形的边长,其中能构成直角三角形的是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 3,4,5 | C. | 6,7,8 | D. | 2,3,4 |
 阅读材料:
阅读材料: