题目内容
4.【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
已知:如图1,在Rt△ABC中,∠C=90°,∠A=30°.
求证:BC=$\frac{1}{2}$AB.
证明:
【灵活运用】该同学家有一张折叠方桌如图2①所示,方桌的主视图如图2②.经测得OA=OB=90cm,OC=OD=30cm,将桌子放平,两条桌腿叉开的角度∠AOB=120°.求:桌面与地面的高度.
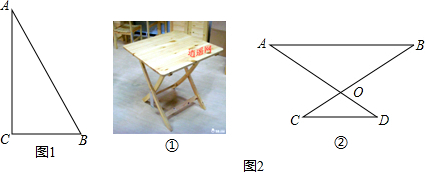
分析 【探究发现】取AB的中点D,连接CD.根据直角三角形的性质得到CD=DB=$\frac{1}{2}$AB,推出△DBC是等边三角形,根据等边三角形的性质即可得到结论;
【灵活运用】:过O作OE⊥AB于E,OF⊥CD于点F根据等腰三角形的性质得到∠A=30°,根据直角三角形的性质即可得到结论.
解答 解:【探究发现】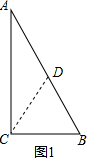
如图1,取AB的中点D,连接CD.
∵在Rt△ABC中,点D是AB的中点,
∴CD=DB=$\frac{1}{2}$AB,
∵∠C=90°,∠A=30°,
∴∠B=60°,
∴△DBC是等边三角形,
∴BC=CD=DB,
∴BC=$\frac{1}{2}$AB;
【灵活运用】:如图②,过O作OE⊥AB于E,OF⊥CD于点F
∵OA=OB,∠AOB=120°
∴∠A=30°,
在Rt△AOE中,OA=90,∠A=30°
∴OE=45,
同理:OF=15,
所以,桌面与地面的高度是60cm.
点评 本题考查了含30°角的直角三角形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
17.计算2×(-3)2的结果是( )
| A. | -12 | B. | 12 | C. | 18 | D. | 36 |
14.下列各组数为三角形的边长,其中能构成直角三角形的是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 3,4,5 | C. | 6,7,8 | D. | 2,3,4 |
 阅读材料:
阅读材料:
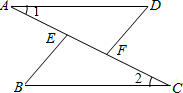 如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.判断BE和DF的位置关系,并说明理由.
如图,已知点A、E、F、C在同一直线上,∠1=∠2,AE=CF,AD=CB.判断BE和DF的位置关系,并说明理由. 如图,已知正六边形ABCDEF内接于⊙O,且边长为4.
如图,已知正六边形ABCDEF内接于⊙O,且边长为4.