题目内容
9.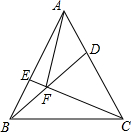 如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.
如图,已知在等边△ABC中,AB=AC=BC=8,点D、E分别是边AC、AB上两点,且AE=CD,BD交CE于F,连接AF,则AF的最小值为$\frac{8\sqrt{3}}{3}$.
分析 由△CAE≌△BCD,推出∠ACE=∠CBD,由∠DFC=∠CBD+∠BCE=∠ACE+∠BCE=60°,推出∠BFC=120°=定值,推出动点F在以O为圆心,OC为半径的圆弧上,此时∠BOC=120°,连接AO,交BC于G,交⊙O于F′,则易知OB=$\frac{8\sqrt{3}}{3}$,AO=2OB=$\frac{16\sqrt{3}}{3}$,当点F与点F′重合时,AF的值最小,由此即可解决问题.
解答 解:如图,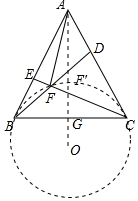
∵△ABC是等边三角形,
∴AC=BC,∠CAE=∠BCD=60°,
在△CAE和△BCD中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACE=∠BCD}\\{AE=CD}\end{array}\right.$,
∴△CAE≌△BCD,
∴∠ACE=∠CBD,
∵∠DFC=∠CBD+∠BCE=∠ACE+∠BCE=60°,
∴∠BFC=120°=定值,
∴动点F在以O为圆心,OC为半径的圆弧上,此时∠BOC=120°,连接AO,交BC于G,交⊙O于F′,
则易知OB=$\frac{8\sqrt{3}}{3}$,AO=2OB=$\frac{16\sqrt{3}}{3}$,当点F与点F′重合时,AF的值最小,最小值为$\frac{8\sqrt{3}}{3}$.
故答案为$\frac{8\sqrt{3}}{3}$.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、圆的有关知识,解题的关键是正确探究动点F的运动轨迹,学会利用辅助圆解决问题,属于中考填空题中的压轴题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1.把多项式x2+ax+b分解因式,得(x-1)(x+3),则a,b的值分别是( )
| A. | a=2,b=3 | B. | a=2,b=-3 | C. | a=-2,b=3 | D. | a=-2,b=-3 |
18.若a、b互为相反数,则a+b-(-2)的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | ±2 |

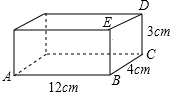 如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少?
如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少? 阅读材料:
阅读材料: