题目内容
7.计算(1)-$\frac{3}{4}$ab2c•(-2a2b)2÷6a2b3
(2)4(x+1)2-(2x-5)(2x+5).
分析 (1)根据单项式的乘法法则进行计算即可;
(2)根据完全平方公式、平方差公式进行计算即可.
解答 解:(1)原式=$-\frac{3}{4}a{b^2}c•4{a^4}{b^2}÷6{a^2}{b^3}$
=-3a5b4c÷6a2b3
=$-\frac{1}{2}{a^3}bc$;
(2)原式=4(x2+2x+1)-(4x2-25)
=4x2+8x+4-4x2+25
=8x+29.
点评 本题考查了整式的混合运算,掌握单项式的乘法法则和完全平方公式、平方差公式是解题的关键.

练习册系列答案
相关题目
17. 如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
 如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 130° | D. | 100° |
2.下列运算正确的是( )
| A. | 3x2+2x3=5x5 | B. | (π-3.14)0=0 | C. | 3-2=-6 | D. | (x3)2=x6 |
17.下列作图语言中,正确的是( )
| A. | 画直线AB=3cm | B. | 延长线段AB到C,使BC=AB | ||
| C. | 画射线AB=5cm | D. | 延长射线OA到B,使AB=OA |
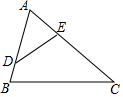 如图,△ABC中,D、E分别是AB、AC边上一点,连接DE.请你添加一个条件,使△ADE∽△ABC,则你添加的这一个条件可以是∠ADE=∠B(写出一个即可).
如图,△ABC中,D、E分别是AB、AC边上一点,连接DE.请你添加一个条件,使△ADE∽△ABC,则你添加的这一个条件可以是∠ADE=∠B(写出一个即可).