题目内容
17. 如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图 A,B,C 是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 130° | D. | 100° |
分析 首先在优弧$\widehat{AC}$上取点D,连接AD,CD,由圆周角定理即可求得∠D的度数,然后由圆的内接四边形的性质,求得∠ABC的度数.
解答  解:如图,在优弧$\widehat{AC}$上取点D,连接AD,CD,
解:如图,在优弧$\widehat{AC}$上取点D,连接AD,CD,
∵∠AOC=100°,
∴∠ADC=$\frac{1}{2}$∠AOC=50°,
∴∠ABC=180°-∠ADC=130°.
故选D.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
12.计算(-9)-(-3)的结果是( )
| A. | -12 | B. | -6 | C. | +6 | D. | 12 |
2.下列命题中,假命题的是( )
| A. | 分别有一个角是110°的两个等腰三角形相似 | |
| B. | 如果两个三角形相似,则他们的面积比等于相似比 | |
| C. | 若5x=8y,则$\frac{x}{y}$=$\frac{8}{5}$ | |
| D. | 有一个角相等的两个菱形相似 |
6.当分式$\frac{x+2}{x-1}$的值为0时,字母x的取值应为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
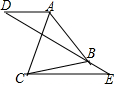 如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.
如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.