题目内容
3.下列说法:①若三角形一边上的中线和这边上的高重合,则这个三角形是等腰三角形;
②全等三角形的中线相等;
③如果直角三角形的两边长分别为3、4,那么斜边长为5;
④两条直角边对应相等的两个直角三角形全等.
其中正确的说法有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 画出图形,根据线段垂直平分线性质得出AB=AC,即可判断①;
根据全等三角形对应边上的中线相等可判断②;
分为两种情况,即可判断③;
根据全等三角形的判定方法即可判断④.
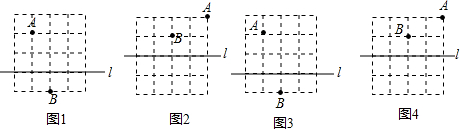
解答 解:①
如图,∵AD是高,
∴AD⊥BC,
∵BD=CD,
∴AB=AC,即△ABC是等腰三角形,
故正确;
②全等三角形对应边上的中线相等,
故错误;
③可能斜边是4,一条直角边是3,
故错误;
④它们的夹角是直角相等,可以根据边角边定理判定全等,
故正确.
综上所述,正确的结论有2个
故选:B.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,三角形内角和定理等知识点的应用,主要考查学生的推理能力和判断能力.

练习册系列答案
相关题目
13. 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件不能判定△ABC是直角三角形的是( )
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |
11.下列选项中,正确的是( )
| A. | -(x-y)=-x-y | B. | 若3x=4y,则3x+5m=4y+5m | ||
| C. | 若am2=bm2,则a=b | D. | 1÷($\frac{1}{3}$-$\frac{1}{2}$)=1÷$\frac{1}{3}$-1÷$\frac{1}{2}$=3-2=1 |
12.(-5ab)2的化简结果是( )
| A. | -25ab2 | B. | 25a2b2 | C. | -25a2b2 | D. | 25a2b |

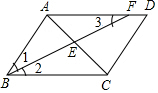 如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.若AB=3,BC=5,求$\frac{AE}{AC}$的值.
如图,在平行四边形ABCD中,∠ABC的平分线BF分别与AC、AD交于点E、F.若AB=3,BC=5,求$\frac{AE}{AC}$的值.