题目内容
15. 二次函数y=ax2+bx+c的图象如图所示,不求函数解析式,根据图象解答下列问题:
二次函数y=ax2+bx+c的图象如图所示,不求函数解析式,根据图象解答下列问题:(1)写出方程ax2+bx+c=0的两个根;
(2)写出式子a+b+c与4a+2b+c的值;
(3)分别指出y>0与y<0时自变量x的取值范围.
分析 (1)找到抛物线与x轴的交点的坐标,即可得出方程ax2+bx+c=0的两个根;
(2)由图象上的点(1,0),(2,2)即可得出结果.
(3)分别寻找抛物线在x轴上方、x轴下方时x的取值范围即可.
解答 解:(1)由图象可得:二次函数的图象与x轴的交点坐标为(1,0),(3,0),
∴方程ax2+bx+c=0的两个根为x1=1,x2=3;
(2)∵二次函数的图象与x轴的一个交点坐标为(1,0),
即当x=1时,y=0,
∴a+b+c=0;
∵顶点坐标为(2,2),
即x=2时,y=2,
∴4a+2b+c=2;
(3)结合图象可得:1<x<3时,y>0;
x<1或x>3时,y<0.
点评 本题考查了抛物线与x轴的交点的问题,此类题目要求学生能结合图象进行判断,注意数形结合,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.若△ABC≌△DEF,△ABC的周长为100,AB=30,EF=25,则AC=( )
| A. | 55 | B. | 45 | C. | 30 | D. | 25 |
7.若a+b<0,且$\frac{a}{b}<0$,则( )
| A. | a,b异号且负数的绝对值大 | B. | a,b异号且正数的绝对值大 | ||
| C. | a>0,b>0 | D. | a<0,b<0 |
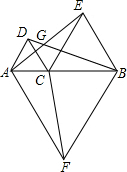 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
 如图:AB、CD分别是⊙O的直径与弦,且AB⊥CD,∠B=30°,判断△ACD的形状,并说明理由.
如图:AB、CD分别是⊙O的直径与弦,且AB⊥CD,∠B=30°,判断△ACD的形状,并说明理由.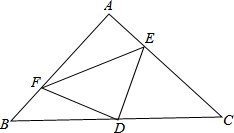 如图,在Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.求证:
如图,在Rt△ABC中,∠BAC=90°,AB=AC,D是BC的中点,AE=BF.求证: