题目内容
1.先化简再求值:($\frac{3}{x-1}$-x-1)÷$\frac{x-2}{{x}^{2}-2x+1}$,其中x是不等式组$\left\{\begin{array}{l}{x-3(x-2)≥2}\\{4x+2<5x+3}\end{array}\right.$的一个整数解.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=$\frac{3-{x}^{2}+1}{x-1}$•$\frac{(x-1)^{2}}{x-2}$
=$\frac{-(x+2)(x-2)}{x-1}$•$\frac{{(x-1)}^{2}}{x-2}$
=-(x+2)(x-1),
解不等式组$\left\{\begin{array}{l}x-3(x-2)≥2\\ 4x+2<5x+3\end{array}\right.$得,-1<x≤2,
当x=0时,原式=-(0+2)(0-1)=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
9.下列语句中正确的是( )
| A. | 正整数、负整数统称为整数 | B. | 正分数、负分数统称为有理数 | ||
| C. | 零既可是正整数也可是负分数 | D. | 所有的分数都是有理数 |
13.下列命题中,真命题有( )个
①三角形有且只有一个外接圆,圆有且只有一个内接三角形;
②如果两条弧不等,那么它们所对的弦也不等;
③如果两条弦相等,那么它们所对的圆周角相等;
④如果两个圆心角相等,那么它们所对的弧相等.
①三角形有且只有一个外接圆,圆有且只有一个内接三角形;
②如果两条弧不等,那么它们所对的弦也不等;
③如果两条弦相等,那么它们所对的圆周角相等;
④如果两个圆心角相等,那么它们所对的弧相等.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
10.在数3.8,-(-10),2π,-|-$\frac{22}{7}$|,0,-22中,正数的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
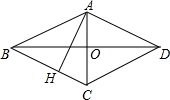 如图,在平行四边形ABCD中,对角线AC与BD相交于O,AC=2,BD=4.AB=$\sqrt{5}$,则平行四边形ABCD的高AH的长为$\frac{4\sqrt{5}}{5}$.
如图,在平行四边形ABCD中,对角线AC与BD相交于O,AC=2,BD=4.AB=$\sqrt{5}$,则平行四边形ABCD的高AH的长为$\frac{4\sqrt{5}}{5}$.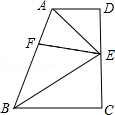 如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分
如图,在直角梯形ABCD中,AD∥BC,∠D=∠C=90°,点E在DC上,且AE,BE分别平分