题目内容
 如图,将一副三角板的直角顶点重合放置于A处,两块三角板可以在同一平面内自由的转动;
如图,将一副三角板的直角顶点重合放置于A处,两块三角板可以在同一平面内自由的转动;(1)当AD是∠CAB的平分线时,试确定AD与BC的位置关系;
(2)试判断∠CAD与∠EAB是否存在大小关系,并说明理由.
考点:角的计算
专题:
分析:(1)设AD与BC交点为F,AD平分∠CAB,得∠DAB=45°,再证出∠DFB=90°即可;
(2)存在;由题意知∠DAB与∠CAD=90°互余,∠EAC与∠CAD互余,容易证出∠EAB+∠CAD=180°.
(2)存在;由题意知∠DAB与∠CAD=90°互余,∠EAC与∠CAD互余,容易证出∠EAB+∠CAD=180°.
解答:解:(1)AD⊥BC;设AD与BC交点为F,如图所示:
 根据题意得,∠CAB=90°,∠B=45°,
根据题意得,∠CAB=90°,∠B=45°,
∵AD平分∠CAB,∴∠DAB=45°,
∴∠DFB=∠B+∠DAB=45°+45°=90°,
∴AD⊥BC;
(2)存在;∠EAB+∠CAD=180°;
理由:∵∠CAB=∠EAD=90°,
∴∠DAB+∠CAD=90°,∠EAC+∠CAD=90°,
∴∠DAB+∠CAD+∠EAC+∠CAD=90°+90°=180°,
∴∠EAB+∠CAD=180°.
 根据题意得,∠CAB=90°,∠B=45°,
根据题意得,∠CAB=90°,∠B=45°,∵AD平分∠CAB,∴∠DAB=45°,
∴∠DFB=∠B+∠DAB=45°+45°=90°,
∴AD⊥BC;
(2)存在;∠EAB+∠CAD=180°;
理由:∵∠CAB=∠EAD=90°,
∴∠DAB+∠CAD=90°,∠EAC+∠CAD=90°,
∴∠DAB+∠CAD+∠EAC+∠CAD=90°+90°=180°,
∴∠EAB+∠CAD=180°.
点评:本题考查了角的计算和角的平分线的定义,弄清各个角之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列事件中的不可能事件是( )
| A、抛一枚硬币,落地后国徽一面朝下 |
| B、随意翻一下日历,翻到的号数是偶数 |
| C、这个月有雨 |
| D、今年夏天的最高气温达到了100℃ |
 如图,已知AB=AC,AD=AE,DB与CE相交于O.
如图,已知AB=AC,AD=AE,DB与CE相交于O. 如图,直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,将纸片沿AD折叠,使C点与AB边上的点E重合.
如图,直角三角形纸片ABC中,∠C=90°,AC=6,BC=8,将纸片沿AD折叠,使C点与AB边上的点E重合.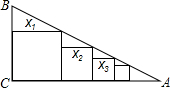 已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第2015个正方形的边长为
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第2015个正方形的边长为
 如图所示,直线AB、CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠AOE=50°,求∠COB和∠BOF的大小各为多少?
如图所示,直线AB、CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠AOE=50°,求∠COB和∠BOF的大小各为多少? 已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=
已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=


