Question

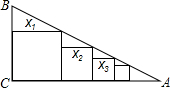已知Rt△ABC中，∠C=90°，BC=1，AC=4，如图把边长分别为x₁，x₂，x₃，…，x_n的n个正方形依次放入△ABC中，则第2015个正方形的边长为

 

．

Answer 1

考点：相似三角形的判定与性质,正方形的性质

专题：规律型

分析：由平行线证出三角形相似，得出比例式，求出第一个正方形的边长为

4

5

，同理求出第二个正方形的边长为(

4

5

)2，得出规律，第2015个正方形的边长为(

4

5

)2015．

解答：解：如图所示：
根据题意得：DE∥CA，
∴△BDE∽△BCA，
∴

DE

CA

=

BD

BC

，即

x1

4

=

1-x1

1

，
解得 x1=

4

5

，
∴EN=

4

5

，NA=4-

4

5

=

16

5

，EF=

4

5

-x2，
∵FG∥CA，
∴△EFG∽△ENA，
∴

FG

NA

=

EF

EN

，即

x2

16 5

=

4 5 -x2

4 5

，
解得 x2=

16

25

=(

4

5

)2，…，
∴第2015个正方形的边长为(

4

5

)2015．
故答案为：(

4

5

)2015．

点评：本题考查了正方形的性质和相似三角形的判定与性质；由三角形相似得出比例式是解题的关键．