题目内容
9. 如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
如图,线段MN表示一段高架道路,线段AB表示高架道路旁的一排居民楼.已知点A到MN的距离为15m,BA的延长线与MN相交于点D,且∠BDN=30°.若汽车沿着从M到N的方向在MN上行驶,方圆39m以内会受到噪音的影响,当其到达点P时,噪音开始影响这一排的居民楼;当其到达点Q时,它与这一排居民楼的距离为39m,求PQ的长度(精确到1m)(参考数据:$\sqrt{3}$≈1.7)
分析 连接PA.在直角△PAH中利用勾股定理来求PH的长度;通过解Rt△ADH、Rt△CDQ分别求得DH、DQ的长度,然后结合图形得到:PQ=PH+DQ-DH,把相关线段的长度代入求值即可.
解答 解:如图,连接PA,作AH⊥MN于H,作QC⊥AB于C.
由题意知,AP=39m.
在直角△APH中,PH=$\sqrt{A{P}^{2}-A{H}^{2}}$=$\sqrt{3{9}^{2}-1{5}^{2}}$=36(m);
在Rt△ADH中,DH=AH•cot30°=15$\sqrt{3}$(m).
在Rt△CDQ中,DQ=$\frac{CQ}{sin30°}$=$\frac{39}{\frac{1}{2}}$=78(m).
则PQ=PH+HQ=PH+DQ-DH=36+78-15$\sqrt{3}$≈114-15×1.7=88.5≈89(m).
答:PQ的长度约为89m.
点评 本题考查了解直角三角形的应用、勾股定理的应用.根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.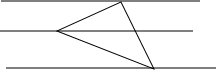 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
18. 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )| A. | 70° | B. | 60° | C. | 40° | D. | 20° |
 一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中和“文”相对的字是强.
一个正方体的每个面上都写有一个汉字,其平面展开图如图所示,那么在该正方体中和“文”相对的字是强.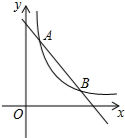 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点. 如图,点A,O,B在同一条直线上,∠COB=20°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为70°或110°.
如图,点A,O,B在同一条直线上,∠COB=20°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为70°或110°.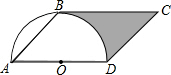 如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).
如图,已知?ABCD,∠A=45°,AD=4,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积为6-π(结果保留π).