题目内容
6. 如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.
如图,⊙O为△ABC的外接圆,直线l与⊙O相切与点P,且l∥BC.(1)请仅用无刻度的直尺,在⊙O中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法);
(2)请写出证明△ABC被所作弦分成的两部分面积相等的思路.
分析 (1)连结PO并延长交BC于E,过点A、E作弦AD即可;
(2)由于直线l与⊙O相切于点P,根据切线的性质得OP⊥l,而l∥BC,则PE⊥BC,根据垂径定理得BE=CE,所以弦AE将△ABC分成面积相等的两部分.
解答  解:(1)如图所示:
解:(1)如图所示:
(2)∵直线l与⊙O相切与点P,
∴OP⊥l,
∵l∥BC,
∴PE⊥BC,
∴BE=CE,
∴弦AE将△ABC分成面积相等的两部分.
点评 此题主要考查了复杂作图,以及切线的性质,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图.

练习册系列答案
相关题目
16. 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )| A. | 2α-60° | B. | 360°-4α | C. | α | D. | 180°-2α |
14.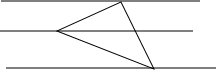 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
18. 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
 如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )
如图,已知AB=CD,BC=AD,∠B=20°,则∠D=( )| A. | 70° | B. | 60° | C. | 40° | D. | 20° |
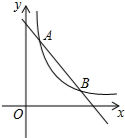 如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+5的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点. 如图,点A,O,B在同一条直线上,∠COB=20°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为70°或110°.
如图,点A,O,B在同一条直线上,∠COB=20°,若从点O引出一条射线OD,使OD⊥OC,则∠AOD的度数为70°或110°.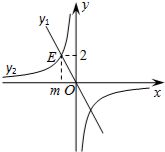 如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2).
如图,正比例函数y1=-2x与反比例函数y2相交于点E(m,2). 如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为2$\sqrt{5}$-2.
如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为2$\sqrt{5}$-2.