题目内容
4. 高铁的开通,给滕州市民带来了极大的方便,“元旦”期间,乐乐和明明相约到济南的某游乐园游玩,乐乐乘私家车从滕州出发1小时后,明明乘坐高铁从滕州出发,先到济南火车西站,然后再乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开滕州的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象解决下面问题:
高铁的开通,给滕州市民带来了极大的方便,“元旦”期间,乐乐和明明相约到济南的某游乐园游玩,乐乐乘私家车从滕州出发1小时后,明明乘坐高铁从滕州出发,先到济南火车西站,然后再乘出租车到游乐园(换车时间忽略不计),两人恰好同时到达游乐园,他们离开滕州的距离y(千米)与乘车时间t(小时)的关系如图所示,请结合图象解决下面问题:(1)求明明乘高铁路线的y与t的函数关系式;
(2)当明明到达济南火车西站时,乐乐距离游乐园还有多少千米?
(3)若乐乐要提前18分钟到达游乐园,问私家车的速度必须达到多少千米/小时?
分析 (1)由待定系数法求出明明乘高铁路线的y与t的函数关系式即可;
(2)求出乐乐乘私家车的y与x的函数解析式,进而求出2小时乐乐行驶的距离,进而得出距离游乐园的路程;
(3)把y=216代入y=80t,得t=2.7,进而求出私家车的速度.
解答 解:(1)设明明乘高铁路线的y与t的函数关系式为y=kt+b,
当t=1时,y=0,当t=2时,y=240,
得:$\left\{\begin{array}{l}{k+b=0}\\{2k+b=240}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=240}\\{b=-240}\end{array}\right.$,
∴明明乘高铁路线的y与t的函数关系式为y=240t-240;
(2)把t=1.5代入y=240t-240,得y=120,
设乐乐乘私家车的y与x的函数关系式为y=at,
当t=1.5,y=120,得1.5t=120,解得:a=80,
∴y=80t,
当t=2,y=160,216-160=56(千米),
∴乐乐距离游乐园还有56千米;
(3)把y=216代入y=80t,得t=2.7,
2.7-$\frac{18}{60}$=2.4(小时),$\frac{216}{2.4}$=90(千米/时).
∴乐乐要提前18分钟到达游乐园,私家车的速度必须达到90千米/小时.
点评 此题主要考查了一次函数的应用、用待定系数法求一次函数的解析式;根据题意结合函数图象得出一次函数解析式是解题关键.

练习册系列答案
相关题目
15.正八边形的每个外角的度数是( )
| A. | 18° | B. | 36° | C. | 45° | D. | 60° |
9.下面图形中,三棱柱的平面展开图为( )
| A. |  | B. |  | C. |  | D. |  |
16. 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
 如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )
如图,已知O为直线AB上一点,OC平分∠BOD,∠AOE=2∠DOE,∠COE=α,则∠AOE的度数为( )| A. | 2α-60° | B. | 360°-4α | C. | α | D. | 180°-2α |
13.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.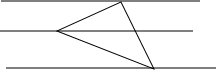 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
 如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )| A. | 3 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |