题目内容
如图，□ABCD中，AE=EF=FB，BG=2CG，DE、DF分别交AG于点P，Q，则EP：PD=考点：平行线分线段成比例,正方形的性质
专题：计算题
分析：延长AG交DC的延长线于M，如图，设正方形的边长为3a，则AE=a，AF=2a，BG=2a，CG=a，在Rt△ABG中，根据勾股定理计算出AG=
a，由AB∥CM，根据平行线分线段成比例定理得
=
，可计算出CM=
a，则DM=DC+CM=
a；再由AE∥DM得到
=
=
；接着在Rt△AMD中，利用勾股定理计算出AM=
a，然后由AF∥DM得到
=
=
，再利用比例性质可计算出AQ=
a，则QG=AG-AQ=
a，于是可计算出
=
．
| 13 |
| AB |
| CM |
| BG |
| CG |
| 3 |
| 2 |
| 9 |
| 2 |
| EP |
| PD |
| AE |
| DM |
| 2 |
| 9 |
3
| ||
| 2 |
| AQ |
| QM |
| AF |
| DM |
| 4 |
| 9 |
6
| ||
| 13 |
7
| ||
| 13 |
| AQ |
| QG |
| 6 |
| 7 |
解答：解：延长AG交DC的延长线于M，如图，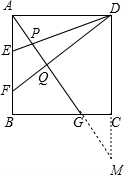
设正方形的边长为3a，则AE=a，AF=2a，BG=2a，CG=a，
在Rt△ABG中，AG=
=
a，
∵AB∥CM，
∴
=
，即
=
，解得CM=
a，
∴DM=DC+CM=
a，
∵AE∥DM，
∴
=
=
=
；
在Rt△AMD中，AM=
=
a，
∵AF∥DM，
∴
=
=
=
，
∴
=
，
∴AQ=
a，
∴QG=AG-AQ=
a，
∴
=
．
故答案为
；
．
设正方形的边长为3a，则AE=a，AF=2a，BG=2a，CG=a，
在Rt△ABG中，AG=
| AB2+BG2 |
| 13 |
∵AB∥CM，
∴
| AB |
| CM |
| BG |
| CG |
| 3a |
| CM |
| 2a |
| a |
| 3 |
| 2 |
∴DM=DC+CM=
| 9 |
| 2 |
∵AE∥DM，
∴
| EP |
| PD |
| AE |
| DM |
| a | ||
|
| 2 |
| 9 |
在Rt△AMD中，AM=
| AD2+DM2 |
3
| ||
| 2 |
∵AF∥DM，
∴
| AQ |
| QM |
| AF |
| DM |
| 2a | ||
|
| 4 |
| 9 |
∴
| AQ |
| AQ+QM |
| 4 |
| 13 |
∴AQ=
6
| ||
| 13 |
∴QG=AG-AQ=
7
| ||
| 13 |
∴
| AQ |
| QG |
| 6 |
| 7 |
故答案为
| 2 |
| 9 |
| 6 |
| 7 |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．也考查了正方形的性质．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，抛物线y=ax2+bx+c与x轴相交于B（2，0）、C（8，0）两点，与y轴的正半轴相交于点A，过点A、B、C三点的⊙P与y轴相切于点A，M为y轴负半轴上的一个动点，直线MB交抛物线于点N，交⊙P于点D．
已知一次函数y=kx+b与反比例函数y=
的概率是0.5，即在一次试验中每个电子元件的状态有两个可能（通电、断开），并且这两个状态的可能行相等．
