题目内容
若（x-2）2+|y+1|=0，则x2+y3= ．
考点：非负数的性质：偶次方,非负数的性质：绝对值
专题：
分析：根据非负数的性质列式求出x、y的值，然后代入代数式进行计算即可得解．
解答：解：由题意得，x-2=0，y+1=0，
解得x=2，y=-1，
所以，x2+y3=22+（-1）3=4-1=3．
故答案为：3．
解得x=2，y=-1，
所以，x2+y3=22+（-1）3=4-1=3．
故答案为：3．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知方程x2-3x+1=0的两根是x1，x2，则
+
=（ ）
| x | 2 1 |
| x | 2 2 |
| A、9 | B、8 | C、7 | D、3 |
在12，-20，-1
，0，-（-5）2，-|+3|中负数的个数有 （ ）
| 1 |
| 2 |
| A、5个 | B、4个 | C、3个 | D、2个 |
下列说法错误的是（ ）
| A、近似数0.8与0.80表示的意义不同 |
| B、近似数2千万和2000万的精确度不一样 |
| C、3.450×104是精确到十位的近似数 |
| D、49554精确到万位是4.9×105 |
在实数
，-
，-3.14，0，π，2.161161116，
中，无理数有（ ）
| 22 |
| 7 |
| 3 |
| 3 | 64 |
| A、1个 | B、2个 | C、3个 | D、4个 |
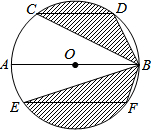如图，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8．则图中阴影部分的面积为