题目内容
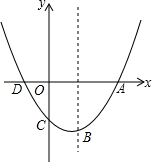 如图,已知抛物线y=
如图,已知抛物线y=| 3 |
| 8 |
| 3 |
| 4 |
(1)若点M在抛物线上,使△MAD的面积与△CAD的面积相等,求点M的坐标.
(2)若点B是抛物线上的一个动点,是否存在某个位置,使BC+BD的值最小?若存在,求出此时的坐标和BC+BD的最小值;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)由抛物线的解析式,可求出点A、D与C的坐标.利用当△MAD的面积与△CAD的面积相等时,分两种情况①点M在x轴下方时,根据抛物线的对称性,②点M在x轴上方时,根据三角形的等面积法,求解即可,
(2)利用当点B与点C或D重合时BC+BD的值最小即可.
(2)利用当点B与点C或D重合时BC+BD的值最小即可.
解答:解:(1)∵y=
x2-
x-3,
∴当y=0时,
x2-
x-3=0,
解得x1=-2,x2=4.
当x=0,y=-3.
∴A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
∵y=
x2-
x-3,
∴对称轴为直线x=1.
∵点A,点D在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,-3),
∴M点坐标为(2,-3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.
当y=3时,
x2-
x-3=3,
解得x1=1+
,x2=1-
,
∴M点坐标为(1+
,3)或(1-
,3).
综上所述,所求M点坐标为(2,-3)或(1+
,3)或(1-
,3).
(2)结论:存在.
当点B与点C或D重合时BC+BD的值最小.
∵D点坐标为(-2,0),C点坐标为(0,-3);
∴点B坐标为(-2,0)或(0,-3);
∴BC+BD=CD=
=
.
| 3 |
| 8 |
| 3 |
| 4 |
∴当y=0时,
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=-2,x2=4.
当x=0,y=-3.
∴A点坐标为(4,0),D点坐标为(-2,0),C点坐标为(0,-3);
∵y=
| 3 |
| 8 |
| 3 |
| 4 |
∴对称轴为直线x=1.
∵点A,点D在x轴上,点M在抛物线上,
∴当△MAD的面积与△CAD的面积相等时,分两种情况:
①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,
∵C点坐标为(0,-3),
∴M点坐标为(2,-3);
②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.
当y=3时,
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=1+
| 17 |
| 17 |
∴M点坐标为(1+
| 17 |
| 17 |
综上所述,所求M点坐标为(2,-3)或(1+
| 17 |
| 17 |
(2)结论:存在.
当点B与点C或D重合时BC+BD的值最小.
∵D点坐标为(-2,0),C点坐标为(0,-3);
∴点B坐标为(-2,0)或(0,-3);
∴BC+BD=CD=
| 22+32 |
| 13 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
相关题目
在12,-20,-1
,0,-(-5)2,-|+3|中负数的个数有 ( )
| 1 |
| 2 |
| A、5个 | B、4个 | C、3个 | D、2个 |
在实数
,-
,-3.14,0,π,2.161161116,
中,无理数有( )
| 22 |
| 7 |
| 3 |
| 3 | 64 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,抛物线y=ax2+bx+c与x轴相交于B(2,0)、C(8,0)两点,与y轴的正半轴相交于点A,过点A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于点N,交⊙P于点D.
如图,抛物线y=ax2+bx+c与x轴相交于B(2,0)、C(8,0)两点,与y轴的正半轴相交于点A,过点A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于点N,交⊙P于点D. 的概率是0.5,即在一次试验中每个电子元件的状态有两个可能(通电、断开),并且这两个状态的可能行相等.
的概率是0.5,即在一次试验中每个电子元件的状态有两个可能(通电、断开),并且这两个状态的可能行相等.
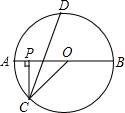 如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究
如图,P是⊙O的直径AB上的一点,PC⊥AB,PC交⊙O于C,∠OCP的平分线交⊙O于D,若点P在半径OA(不包括O点和A点)上移动时,试探究