题目内容
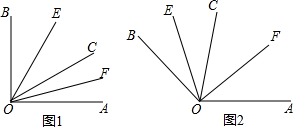
5.已知∠AOB内部有三条射线,其中OE平分∠BOC,OF平分∠AOC.(1)如图1,若∠AOB=90°,∠AOC=30°,求EOF的度数;
(2)如图2,若∠AOB=α,求∠EOF的度数(用含α的式子表示);
(3)若将题中的“OE平分∠BOC,OF平分∠AOC”的条件改为“∠EOB=$\frac{1}{3}$∠BOC,∠COF=$\frac{2}{3}$∠AOC”,且∠AOB=α,求∠EOF的度数(用含α的式子表示)
分析 (1)首先求得∠BOC的度数,然后根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF即可求解;
(2)根据角的平分线的定义和角的和差可得∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC+∠AOC),即可求解;
(3)根据角的等分线的定义可得∠EOF=∠EOC+∠COF=$\frac{2}{3}$∠BOC+$\frac{2}{3}$∠AOC=$\frac{2}{3}$(∠BOC+∠AOC)=$\frac{2}{3}$∠AOB,即可求解.
解答 解:(1)∠BOC=∠AOB-∠AOC=90°-30°=60°,
∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°,∠COF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×30°=15°,
∴∠EOF=∠EOC+∠COF=30°+15°=45°;
(2)∵OE平分∠BOC,OF平分∠AOC,
∴∠EOC=$\frac{1}{2}$∠BOC,∠COF=$\frac{1}{2}$∠AOC,
∴∠EOF=∠EOC+∠COF=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB=$\frac{1}{2}$a;
(3)∵∠EOB=$\frac{1}{3}$∠BOC,
∴∠EOC=$\frac{2}{3}$∠BOC,
又∵∠COF=$\frac{2}{3}$∠AOC,
∴∠EOF=∠EOC+∠COF=$\frac{2}{3}$∠BOC+$\frac{2}{3}$∠AOC=$\frac{2}{3}$(∠BOC+∠AOC)=$\frac{2}{3}$∠AOB=$\frac{2}{3}$a.
点评 本题考查了角度的计算,理解角的平分线的定义以及角度的和、差之间的关系是关键.

| 月份 | 一月 | 二月 | 三月 | 四月 | 五月 | 六月 | 七月 |
| 钱数变化 | +300 | +220 | -150 | -100 | +330 | +200 | +280 |
(2)请判断七个月以来小红得到奖金最多是哪个月?最少是哪个月?它们相差多少元?
(3)若2015年这七个月中小红最多得到的奖金是2800元,请问2014年12月份她得到多少奖金?
| A. | $\sqrt{(-2)^{2}}$=2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | $\sqrt{4}$=±2 | D. | $\root{3}{8}$=±2 |
| A. | $\frac{1}{2}$cm | B. | 1cm | C. | 4cm | D. | 2cm |
 如图,点A、O、B在同一直线上,OD平分∠AOC,OE平分∠BOC.
如图,点A、O、B在同一直线上,OD平分∠AOC,OE平分∠BOC. 如图,在∠AOB内有一点C.
如图,在∠AOB内有一点C.