题目内容
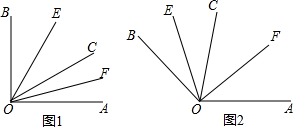
20. 如图,点A、O、B在同一直线上,OD平分∠AOC,OE平分∠BOC.
如图,点A、O、B在同一直线上,OD平分∠AOC,OE平分∠BOC.(1)图中∠AOD的补角是∠BOD,∠BOE的补角是∠AOE;
(2)∠COD与∠EOC具有的数量关系是∠COD+∠EOC=90°;
(3)若∠AOC=62°18′,求∠COD和∠BOE的度数.
分析 (1)根据补角定义得出即可;
(2)求出∠AOC+∠BOC=180°,∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}∠$BOC,即可求出答案;
(3)根据角平分线定义即可求出∠COD,求出∠BOC,再根据角平分线定义求出即可.
解答 解:(1)∠AOD的补角为∠BOD,∠BOE的补角为∠AOE,
故答案为:∠BOD,∠AOE;
(2)∠COD+∠EOC=90°,
理由是:∵点A、O、B在同一直线上,
∴∠AOC+∠BOC=180°,
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC,∠EOC=$\frac{1}{2}∠$BOC,
∴∠COD+∠EOC=$\frac{1}{2}$×180°=90°,
故答案为:∠COD+∠EOC=90°;
(3)∵OD平分∠AOC,
∴∠COD=$\frac{1}{2}$∠AOC,
∵∠AOC=62°18′,
∴∠COD=$\frac{1}{2}$×62°18′=31°9′,
又∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC,
∵∠BOC=180°-∠AOC
=180°-62°18′=117°42′,
∴∠BOE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×117°42′=58°51′.
点评 本题考查了余角和补角,角平分线定义的应用,能知道∠α的补角为180°-∠α和角平分线定义是解此题的关键.

练习册系列答案
相关题目
11.有一列数a1,a2,a3,a4,a5,…,an,其中,a1=3×2+1,a2=3×3+2,a3=3×4+3,a4=3×5+4,a5=3×6+5,…,当an=2015时,n的值等于( )
| A. | 503 | B. | 502 | C. | 501 | D. | 500 |
15.方程(x-1)(x-3)=5化为ax2+bx+c=0形式后,a,b,c的值分别为( )
| A. | 1,4,3 | B. | 1,-4,3 | C. | 1,-4,-2 | D. | 1,-4,2 |
 在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A的右侧),与轴交于点C,tan∠CBA=$\frac{1}{2}$.
在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A的右侧),与轴交于点C,tan∠CBA=$\frac{1}{2}$. 如图,在平面内有四个点A,B,C,D,请你用直尺按下列要求作图.
如图,在平面内有四个点A,B,C,D,请你用直尺按下列要求作图.