题目内容
16.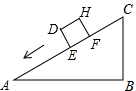 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.| A. | $\frac{16}{3}$ | B. | $\frac{14}{3}$ | C. | 5 | D. | 4 |
分析 根据已知得出设AE=x米,可得EC=(12-x)米,利用勾股定理得出DC2=DE2+EC2=4+(12-x)2,AE2+BC2=x2+36,即可求出x的值.
解答  解:如图,连接CD,
解:如图,连接CD,
设AE=x米,
∵坡角∠A=30°,∠B=90°,BC=6米,
∴AC=12米,
∴EC=(12-x)米,
∵正方形DEFH的边长为2米,即DE=2米,
∴DC2=DE2+EC2=4+(12-x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(12-x)2=x2+36,
解得:x=$\frac{14}{3}$米,
答:当AE为$\frac{14}{3}$米时,有DC2=AE2+BC2
故选:B.
点评 此题主要考查了勾股定理的应用以及一元二次方程的应用,根据已知表示出CE,AE的长度是解决问题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
7.下列运算正确的是( )
| A. | a+a=a2 | B. | a2•a=a2 | C. | a3÷a2=a (a≠0) | D. | (a2)3=a5 |
8.某水果店有甲、乙两种苹果包装盒,现有360个苹果要用这两种包装盒进行包装,已知每个甲包装盒比每个乙
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
包装盒少装3个苹果,单独用甲包装盒比单独用乙包装盒多用6个,设每个甲包装盒可装x个苹果,根据题意
下面所列方程正确的是( )
| A. | $\frac{360}{x}$=$\frac{360}{x-3}$+6 | B. | $\frac{360}{x}$=$\frac{360}{x+3}$+6 | C. | $\frac{360}{x-3}$=$\frac{360}{x}$+6 | D. | $\frac{360}{x+3}$=$\frac{360}{x}$+6 |
6. 如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
 如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
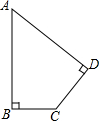 如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长.
如图,已知一块四边形草地ABCD,其中∠A=45°,∠B=∠D=90°,AB=2m,CD=1m.求这块草地的面积和周长. 如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.
如图,某校把一块三角形的废地ABC改建成一个花园,测得AC=80cm,BC=60cm,AB=100cm.