题目内容
6. 如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )
如图,在等腰梯形ABCD中,AC,BD相交于点O,则图中全等三角形的对数有( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 结合等腰梯形的性质和全等三角形的判定和性质可求得答案.
解答 解:
∵四边形ABCD为等腰梯形,
∴AD=BC,AC=BD,
在△ABC和△BAD中
$\left\{\begin{array}{l}{AB=BA}\\{AC=BD}\\{BC=AD}\end{array}\right.$
∴△ABC≌△BAD(SSS),
同理可证得△ACD≌△BDC,
∴OC=OD,OB=OA,
在△BOC和△AOD中
$\left\{\begin{array}{l}{BO=AO}\\{CO=DO}\\{BC=AD}\end{array}\right.$
∴△BOC≌△AOD(SSS),
∴全等三角形的对数有3对,
故选D.
点评 本题主要考查等腰梯形的性质和全等三角形的判定方法,掌握等腰梯形的两腰相等、对角线相等是解题的关键.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
16.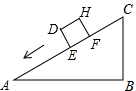 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
 一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.
一个正方体物件沿斜坡向下滑动,截面如图所示,正方体DEFH的边长为2米,∠A=30°,∠B=90°,BC=6米,则当AE=( )米时,有DC2=AE2+BC2.| A. | $\frac{16}{3}$ | B. | $\frac{14}{3}$ | C. | 5 | D. | 4 |
14. 如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
 如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )
如图,已知四边形ABCD是正方形,P是直线AD上一动点,使△PBC是等腰三角形的点P有( )| A. | 1个 | B. | 3个 | C. | 5个 | D. | 7个 |
1.下列各组中的两个项不属于同类项的是( )
| A. | 3x2y和-2x2y | B. | a2和32 | C. | -1和$1\frac{1}{4}$ | D. | -xy和2yx |
18. 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
 如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )
如图,是学校花圃的一角,有的同学为了省时间图方便,在花圃中踩出了一条“捷径”,“捷径”的数学道理是( )| A. | 两点确定一条直线 | B. | 垂线段最短 | ||
| C. | 两点之间,线段最短 | D. | 两点之间,直线最短 |
15.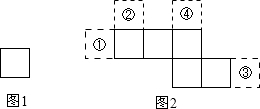 图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
 图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )
图1和图2中所有的正方形都全等,将图1中的正方形放在图2中的①②③④某一位置,所组成的图形能围成正方体的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
16.如果a=b,则下列式子不一定成立的是( )
| A. | a+1=b+1 | B. | $\frac{a}{3}$=$\frac{b}{3}$ | C. | a2=b2 | D. | a-c=c-b |
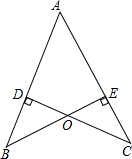 如图CD⊥AB于D,BE⊥AC于E,OD=OE,求证:OB=OC
如图CD⊥AB于D,BE⊥AC于E,OD=OE,求证:OB=OC 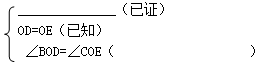
 “共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的统计图,下面有四个推断:
“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小文对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的统计图,下面有四个推断: