题目内容
利用配方法将x2+2x+3=0化为a(x-h)2+k=0(a≠0)的形式为( )
| A、(x-1)2-2=0 |
| B、(x-1)2+2=0 |
| C、(x+1)2+2=0 |
| D、(x+1)2-2=0 |
考点:解一元二次方程-配方法
专题:
分析:根据配方法的步骤在等式两边同时加上一次项系数2的一半的平方,即可把x2+2x+3=0化为a(x-h)2+k=0(a≠0)的形式.
解答:
解:x2+2x+3=0,
x2+2x+1+3=1,
(x+1)2+2=0,
故选C.
x2+2x+1+3=1,
(x+1)2+2=0,
故选C.
点评:此题考查了配方法解一元二次方程,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.

练习册系列答案
相关题目
 如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )
如图,分别以直角三角形ABC的三边作正三角形,已知AC=6,AB=10,阴影部分的面积分别记为S1,S2,S3,则S1+S3-S2的值为( )| A、24 | ||
| B、48 | ||
C、25
| ||
D、50
|
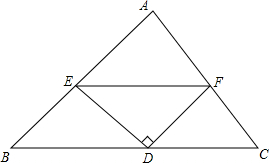 如图,已知△ABC中,D是BC的中点,ED⊥DF.求证:BE+CF>EF.
如图,已知△ABC中,D是BC的中点,ED⊥DF.求证:BE+CF>EF.