已知|x|=1.|y|=2.|z|=3.且xy＜0.xyz＞0.求的值．题目和参考答案——青夏教育精英家教网—

题目内容

6．已知|x|=1，|y|=2，|z|=3，且xy＜0，xyz＞0，求（x+y+z）•（xy+yz）的值．

分析分类讨论：x＞0，y＜0，z＜0；x＜0，y＞0，z＜0；根据绝对值的意义，可得x、y、z的值，根据代数式求值，可得答案．

解答解：由|x|=1，|y|=2，|z|=3，且xy＜0，xyz＞0，得
x=1，y=-2，z=-3，原式=（1-2-3）[（-2）+（-2）×（-3）]=-4×[-2+6]=-4×4=-16；
x=-1，y=2，z=-3，原式=（-1+2-3）[-2+2×（-3）]=-2×[-2+（-6）]=-2×（-8）=16．

点评本题考查了代数式求值，分类讨论是解题关键，以防遗漏．

练习册系列答案

相关题目

16．等腰三角形的顶角为70°，底边上的高为11.3，则腰长为（　　）

17．

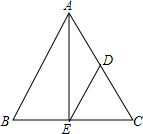如图，△ABC中，AB=AC，点D，E分别在AC，BC上，且DA=DE，DE∥AB，求证：E是BC的中点．

14．

看图填空，如图：
（1）如图中共有4个三角形，它们是△ABC、△EBG、△AEF、△CGF；
（2）△BGE的三个顶点分别是B、G、E，三条边分别是BE、EG、BE，三个角分别是∠B、∠BEG、∠BGE；
（3）△AEF中，顶点A所对的边是EF；边AF所对的顶点是E；
（4）∠ACB是△ACB的内角，∠ACB的对边是AB．

1．已知2²-1²=2+1，3²-2²=3+2，4²-3²=4+3，…
（1）从以上等式中你能发现怎样的规律？（提示：当n为正整数时，（n+1）²-n²=？）
（2）计算201²-200²的值．

11．观察下列各式：
$\frac{1}{1×2}$=$\frac{1}{2}$=1-$\frac{1}{2}$；$\frac{1}{1×3}$=$\frac{1}{3}$=$\frac{1}{2}$×（1-$\frac{1}{3}$）；$\frac{1}{1×4}$=$\frac{1}{4}$=$\frac{1}{3}$×（1-$\frac{1}{4}$）；$\frac{1}{2×3}$=$\frac{1}{6}$=$\frac{1}{2}$-$\frac{1}{3}$；$\frac{1}{3×5}$=$\frac{1}{15}$=$\frac{1}{2}$×（$\frac{1}{3}$-$\frac{1}{5}$）；$\frac{1}{4×7}$=$\frac{1}{28}$=$\frac{1}{3}$×（$\frac{1}{4}$-$\frac{1}{7}$）；…
你能用类似的方法去写$\frac{1}{1×7}$和$\frac{1}{7×13}$吗？你会用含字母的式子表达发现的规律吗？

18．

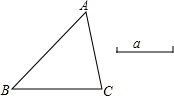已知△ABC和线段a，且a＞$\frac{1}{2}$BC，用直尺和圆规求作⊙O．使⊙O经过B，C两点，且半径为a，并说出可以作出几个圆（要求写出作法）．

15．

如图，在面积为S的正方形ABCD中，E是AB的中点，BF⊥CE，垂足为F，求△BFC的面积．

16．若|a-1|与（b+2）²互为相反数，试求a²⁰¹⁶+（a+b）²⁰¹⁵的值．

试题分类