题目内容
17.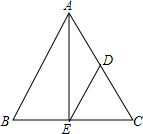 如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点.
如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点.
分析 由DA=DE,得到∠EAD=∠AED,根据平行线的性质得到∠BAE=∠AED,等量代换得到∠BAE=∠EAC,然后根据等腰三角形的性质即可得到结论.
解答 证明:∵DA=DE,
∴∠EAD=∠AED,
∵DE∥AB,
∴∠BAE=∠AED,
∴∠BAE=∠EAC,
∵AB=AC,
∴BE=CE,
∴E是BC的中点.
点评 此题考查了等腰三角形的判定与性质,平行线的性质,关键是根据题意得出∠BAE=∠CAE.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
8.已知x2=9,|y|=8,且xy<0,则x+y的值等于( )
| A. | ±5 | B. | ±11 | C. | -5或11 | D. | -5或-11 |
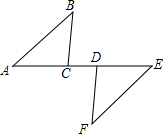 如图,△ABC≌△EFD,∠A与∠E是对应角.
如图,△ABC≌△EFD,∠A与∠E是对应角. 阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系.
阅读下面的证明过程,在括号内填写适当的理由,并在横线上说明其中的因果关系. 如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC.
如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC.