题目内容
1.已知22-12=2+1,32-22=3+2,42-32=4+3,…(1)从以上等式中你能发现怎样的规律?(提示:当n为正整数时,(n+1)2-n2=?)
(2)计算2012-2002的值.
分析 (1)由等式左边两数的平方差,两底数是相邻的两个自然数,右边为两底数的和,由此得出可知,第n个式子为:(n+1)2-n2=2n+1;
(2)利用(1)的规律计算即可.
解答 解:(1)∵22-12=2+1,
32-22=3+2,
42-32=4+3,
…
∴第n个式子为:(n+1)2-n2=2n+1;
(2)2012-2002=201+200=401.
点评 此题考查数字的变化规律,由已知等式发现一般规律,根据一般规律对算式进行计算即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列计算正确的是( )
| A. | 2-3=$\frac{1}{6}$ | B. | ${(-x)}^{-2}=\frac{1}{{x}^{2}}$ | C. | ${x}^{-1}+{y}^{-1}=\frac{1}{x+y}$ | D. | $(\frac{1}{7})^{-2}=\frac{1}{49}$ |

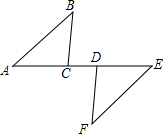 如图,△ABC≌△EFD,∠A与∠E是对应角.
如图,△ABC≌△EFD,∠A与∠E是对应角. 如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC.
如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC. 如图,是某市的部分简图,文化馆在D2区,体育馆在C4区,请将A、B、C、D、E、1、2、3、4、5分别填入相应的小括号里.
如图,是某市的部分简图,文化馆在D2区,体育馆在C4区,请将A、B、C、D、E、1、2、3、4、5分别填入相应的小括号里. 如图,∠DAE=∠CBE,∠EAB=∠EBA,请你写出两个正确的结论:AE=EB,AD=BC.
如图,∠DAE=∠CBE,∠EAB=∠EBA,请你写出两个正确的结论:AE=EB,AD=BC.