题目内容

4．|x-2|-|x-5|的最大值是3，最小值是-3．

分析 可以根据对x的值的范围的讨论，去掉绝对值符号，对式子进行化简．

解答 解：当2≤x≤5时，|x-2|-|x-5|=x-2+（x-5）=2x-7，
则|x-2|-|x-5|的最大值是3，最小值是-3，
当x＜2时，|x-2|-|x-5|=2-x+（x-5）=-3，
则|x-2|-|x-5|是定值-3，
当x＞5时，|x-2|-|x-5|=x-2-（x-5）=3，
则|x-2|-|x-5|是定值3，
∴|x-2|-|x-5|的最大值是3，最小值是-3．
故答案为：3，-3．

点评 此题考查了绝对值的化简，利用分类讨论的方法，把x的取值分为多段，去掉绝对值符号．

练习册系列答案
相关题目
14．点A从数轴上表示+5的位置开始移动，第一次沿数轴先向右移动1个单位长度，再向左移动2个单位长度到达A1点；第二次从点A1开始，沿数轴先向右移动3个单位长度，再向左移动4个单位长度到达点A2；第三次从点A2开始，沿数轴向右移动5个单位长度，再向左移动6个单位长度到达点A3…
（1）数轴上点A1表示的数是+4；
（2）数轴上点A5表示的数是0；
（3）数轴上点8表示的数是-3．
15．根据下列条件，分别确定二次函数的解析式：
（1）抛物线y=ax2+bx+c过点（-3，2），（-1，-1），（1，3）；
（2）抛物线y=ax2+bx+c与x轴的两交点的横坐标分别是-$\frac{1}{2}$，$\frac{3}{2}$，与y轴交点的纵坐标是-5．
12．已知x=$\sqrt{3}$-$\sqrt{2}$，y是x的倒数，则x+y=2$\sqrt{3}$．
19．设x1，x2是方程2x2+4x-3=0的两个根，利用根与系数的关系，求下列各式的值：
（1）$\frac{1}{x_1}+\frac{1}{x_2}$；
（2）（x1+1）（x2+1）；
（3）x12+x22．
8．先写出下列各数，再把写出的数在数轴上表示出来．
（1）-3的相反数；（2）0的相反数；（3）相反数是2$\frac{1}{2}$的数；（4）相反数是-0.5的数．

已知x1，x2是关于x的方程（x﹣2）（x﹣3）=（n﹣2）（n﹣3）的两个实数根．则：

（1）两实数根x1，x2的和是______；

（2）若x1，x2恰是一个直角三角形的两直角边的边长，那么这个直角三角形面积的最大值是______．
2．如图（1）已知△ABC，AB=AC，点E在AB上，作EF∥AB交AC于F．
（1）试给出BE与CF数量关系．
（2）将△AEF绕点A顺时针旋转如图（2），BE交CF于点O
①（1）中的结论还成立吗？请给出并证明你的结论．
②当∠ABC=60°时，∠BOC度数为60°；
当∠ABC=α时，∠BOC度数为α（0°＜α＜90°）
（3）在（2）的基础上，当∠BAC=90°，如图（3），（点B、A、F不在同一直线上），连接CE、BF，当点P为BF中点时，问$\frac{CE}{AP}$的值是否改变？若不变，证明求其值；若变，说明理由．
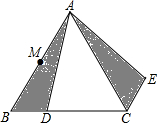3．如图，△ABC是等边三角形，D是BC上一点，△ABD经过逆时针旋转后到达△ACE的位置．
（1）旋转中心是点A，旋转角度60度．
（2）如果M是AB的中点，那么经过上述旋转后，点M转到了什么位置？
（3）连接DE，△ADE是怎样的三角形？为什么？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网