题目内容
 如图已知,在△ABC中,AB=5,AC=6,BC=7,点D、E分别在AB、AC上,DE∥BC,且△ADE的周长与四边形BCED的周长相等,求DE的长.
如图已知,在△ABC中,AB=5,AC=6,BC=7,点D、E分别在AB、AC上,DE∥BC,且△ADE的周长与四边形BCED的周长相等,求DE的长.考点:相似三角形的判定与性质
专题:
分析:根据△ADE的周长与四边形BCED的周长相等,可得AE+AD=BC+CE+DB,不妨设AE+AD=a,CE+DB=b,由题意可得到a和b的方程组,解方程组可求出a的值,再根据相似三角形的性质即可求出DE的长.
解答:解:∵△ADE的周长与四边形BCED的周长相等,
∴AD+AE+ED=BC+EC+DE+DB,即AE+AD=BC+CE+DB,
不妨设AE+AD=a,CE+DB=b,则
,
解得a=9,
即AE+AD=9①,
∵DE∥BC,
∴△ADE∽△ACB,
∴
=
=
②,
由①②,得到AE=
,
∵
=
,
∴DE=
.
∴AD+AE+ED=BC+EC+DE+DB,即AE+AD=BC+CE+DB,
不妨设AE+AD=a,CE+DB=b,则
|

解得a=9,
即AE+AD=9①,
∵DE∥BC,
∴△ADE∽△ACB,
∴
| AE |
| AD |
| AC |
| AB |
| 6 |
| 5 |
由①②,得到AE=
| 21 |
| 4 |
∵
| ED |
| BC |
| AE |
| AC |
∴DE=
| 9 |
| 2 |
点评:本题考查了相似三角形的判定和性质,三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.

练习册系列答案
相关题目
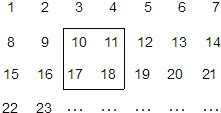 把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.
把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.
 如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上.
如图:方格纸中的每个小正方形边长均为1,△ABC和△DEF的顶点都在方格纸的格点上. 如图,在?ABCD中,请再添加一个条件,使得四边形ABCD是矩形,你所添加的条件是
如图,在?ABCD中,请再添加一个条件,使得四边形ABCD是矩形,你所添加的条件是