题目内容
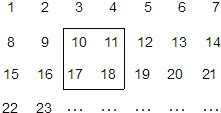 把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.
把2005个正整数1,2,3,4,…,2005按如图方式排列成一个表.(1)如图,用一正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是
(2)当(1)中被框住的4个数之和等于396时,x的值为多少?
(3)在(1)中能否框住这样的4个数,它们的和等于156?若能,则求出x的值;若不能,则说明理由.
(4)从左到右的七列中,第
考点:一元一次方程的应用
专题:
分析:(1)这道题同日历中的数据一样,左右相邻两数相差1,上下两数相差7.求得答案为x+1,x+7,x+8.
(2)在(1)的基础上,列出一元一次方程就可求出;
(3)令(1)中表示的四个数相加,求x的值;
(4)根据2005除以7的余数即可确定;
(2)在(1)的基础上,列出一元一次方程就可求出;
(3)令(1)中表示的四个数相加,求x的值;
(4)根据2005除以7的余数即可确定;
解答:解:(1)由左右相邻两数相差1,上下两数相差7,可以得出左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是x+1,x+7,x+8.
故答案是:x+1,x+7,x+8;
(2)根据题意列方程得:
x+x+1+x+7+x+8=396
解得x=95.
答:当(1)中被框住的4个数之和等于396时,x的值为95;
(3)假设存在,则x+x+1+x+7+x+8=156,
解之得x=35,
∵35位于表中的第4行第7列一个数,
∴不能框住这样的4个数,
故x不存在;
(4)第3列数字和最大;
因为2005÷7等于286余3,所以第3列所有数字和最大;
故答案是:x+1,x+7,x+8;
(2)根据题意列方程得:
x+x+1+x+7+x+8=396
解得x=95.
答:当(1)中被框住的4个数之和等于396时,x的值为95;
(3)假设存在,则x+x+1+x+7+x+8=156,
解之得x=35,
∵35位于表中的第4行第7列一个数,
∴不能框住这样的4个数,
故x不存在;
(4)第3列数字和最大;
因为2005÷7等于286余3,所以第3列所有数字和最大;
点评:本题主要考查了一元一次方程的应用.找出表中数字的规律和等量关系是本题的关键;

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
体育中考前,我区在4500名九年级学生中随机抽取若干名学生进行体能测试,成绩记为1级,2级,3级,4级共4个等级.并将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息估计,我区学生进行体能测试成绩为2级的学生人数是( )


| A、3 | B、6 | C、27 | D、270 |
 如图,正三角形BCO与正三角形EOD是关于原点O的位似图形,位似比为2:1,点B的坐标为(-2,0),则点D的坐标为( )
如图,正三角形BCO与正三角形EOD是关于原点O的位似图形,位似比为2:1,点B的坐标为(-2,0),则点D的坐标为( )| A、(1,0) | ||||||
| B、(1,-1) | ||||||
C、(
| ||||||
| D、(1,-2) |

 已知,如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E,求证:
已知,如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E,求证: 如图已知,在△ABC中,AB=5,AC=6,BC=7,点D、E分别在AB、AC上,DE∥BC,且△ADE的周长与四边形BCED的周长相等,求DE的长.
如图已知,在△ABC中,AB=5,AC=6,BC=7,点D、E分别在AB、AC上,DE∥BC,且△ADE的周长与四边形BCED的周长相等,求DE的长.