题目内容
2.正方形ABCD中,在AB边上有一定点E,AE=3cm,EB=1cm,在AC上有一动点P,若使得EP+BP的和最小,则EP+BP的最短距离为( )| A. | 5cm | B. | 4cm | C. | 3cm | D. | 4.8cm |
分析 连接DE,交直线AC于点P,根据四边形ABCD是正方形可知B、D关于直线AC对称,所以DE的长即为EP+BP的最短距离,再根据勾股定理即可得出结论.
解答  解:连接DE,交直线AC于点P,
解:连接DE,交直线AC于点P,
∵四边形ABCD是正方形,
∴B、D关于直线AC对称,
∴DE的长即为EP+BP的最短距离,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故选A.
点评 本题考查的是轴对称-最短路线问题,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
10. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
7.比较a与-a的大小( )
| A. | a>-a | B. | a<-a | C. | a=-a | D. | 以上都有可能 |
11.已知函数y=3(x-2)2+1图象上有三点A(1,y1)、B(4,y2)、C($\sqrt{2}$,y3),试确定y1、y2、y3的大小( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
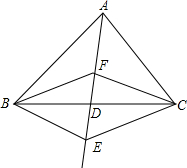 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE. 如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )
如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )



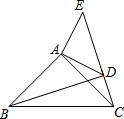 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证:
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证: