题目内容
10. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,然后求出△BEC周长=AC+BC,再根据等腰三角形两腰相等可得AC=AB,代入数据计算即可得解.
解答 解:∵DE是AB的垂直平分线,
∴AE=BE,
∴△BEC周长=BE+CE+BC=AE+CE+BC=AC+BC,
∵腰长AB=8,
∴AC=AB=8,
∴△BEC周长=8+5=13.
故选A.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形两腰相等的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
8.若分式$\frac{a+5}{a-5}$有意义,则a的取值范围是( )
| A. | a=-5 | B. | a≠5 | C. | a=5 | D. | a≠-5 |
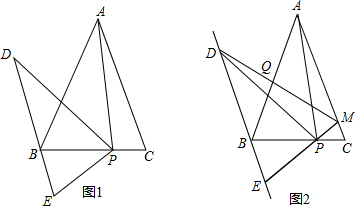
2.正方形ABCD中,在AB边上有一定点E,AE=3cm,EB=1cm,在AC上有一动点P,若使得EP+BP的和最小,则EP+BP的最短距离为( )
| A. | 5cm | B. | 4cm | C. | 3cm | D. | 4.8cm |
 钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)
钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号) 在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)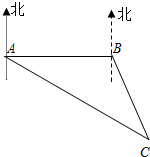 如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)