题目内容
已知t是方程x2-x-1=0的一个解,则-t3+2t2+2002的值为( )
| A、2001 | B、2002 |
| C、2003 | D、2004 |
考点:一元二次方程的解
专题:
分析:根据t是方程x2-x-1=0的一个解,则t2-t-1=0,即t2-t=1,然后把所求的式子利用t2-t=1表示,代入求解.
解答:解:∵t是方程x2-x-1=0的一个解,
∴t2-t-1=0,即t2-t=1,
则-t3+2t2+2002=-(t3-2t2)+2002
=-t(t2-t-t)+2002
=-t(1-t)+2002
=t2-t+2002
=1+2002
=2003.
故选C.
∴t2-t-1=0,即t2-t=1,
则-t3+2t2+2002=-(t3-2t2)+2002
=-t(t2-t-t)+2002
=-t(1-t)+2002
=t2-t+2002
=1+2002
=2003.
故选C.
点评:本题考查了方程的解的定义以及代数式的求值,利用t2-t表示出所求的代数式是关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知a、b、c是三角形的三边,则代数式a2-2ab+b2-c2的值( )
| A、不能确定 | B、大于0 |
| C、等于0 | D、小于0 |
以下列线段a、b、c的长为边,不能构成直角三角形的是( )
| A、a=4,b=5,c=6 | ||
| B、a=10,b=8,c=6 | ||
C、a=2,b=2,c=2
| ||
D、a=1,b=2,c=
|
已知一个菱形的周长是20,两条对角线的比是4:3,则这个菱形的面积是( )
| A、12 | B、24 | C、48 | D、96 |
 如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②2a+b=0;③4a+2b+c>0;④当x>2时,y随x的增大而增大;⑤对于任意x均有ax2+ax-a>b,正确的说法有( )
如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②2a+b=0;③4a+2b+c>0;④当x>2时,y随x的增大而增大;⑤对于任意x均有ax2+ax-a>b,正确的说法有( )| A、5个 | B、4个 | C、3个 | D、2个 |
已知m2-m-1=0,则计算:m4-m3-m+2的结果为( )
| A、3 | B、-3 | C、5 | D、-5 |
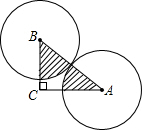 如图所示,在直角△中,C=90°,AC=6,BC=8,两等圆A,B外切,那么图中两个扇形(阴影部分)的面积之和( )
如图所示,在直角△中,C=90°,AC=6,BC=8,两等圆A,B外切,那么图中两个扇形(阴影部分)的面积之和( )A、
| ||
B、
| ||
C、
| ||
| D、25π |