题目内容
6.解方程组:$\left\{{\begin{array}{l}{{x^2}-{y^2}=4}\\{3\sqrt{5}x-5y-10=0}\end{array}}\right.$.分析 把其中的二元一次方程变形,用一个未知数表示另一个未知数,代入二元二次方程,化为一元二次方程,解这个方程,求出未知数,代入二元一次方程求出另一个未知数即可.
解答 解:$\left\{\begin{array}{l}{{x}^{2}-{y}^{2}=4①}\\{3\sqrt{5}x-5y-10=0②}\end{array}\right.$
由②得,y=-$\frac{10-3\sqrt{5}x}{5}$③
把③代入①,得
x2-3$\sqrt{5}$x+10=0
解得x1=2$\sqrt{5}$,x2=$\sqrt{5}$
把x=2$\sqrt{5}$,x=$\sqrt{5}$代入③得y1=4,y2=1.
所以方程组的解为$\left\{\begin{array}{l}{{x}_{1}=2\sqrt{5}}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{5}}\\{{y}_{2}=1}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,解题的关键是灵活运用代入法,实现消元,从而求出方程组的解.

练习册系列答案
相关题目
16.若α为锐角,且sinα=$\frac{4}{5}$,则tanα为( )
| A. | $\frac{9}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
1.从1,2,3,4,5这五个数字任取两个数字,使其乘积为偶数的概率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
11.若M(-$\frac{1}{2}$,y1)、N(-$\frac{1}{4}$,y2)、P($\frac{1}{2}$,y3)三点都在函数y=-$\frac{1}{x}$的图象上,则y1、y2、y3的大小关系为( )
| A. | y2>y3>y1 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
18. 如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
 如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )
如图,直线a∥b,直线a、b被直线c所截,∠1=40°,则∠2的度数为( )| A. | 40° | B. | 80° | C. | 140° | D. | 160° |
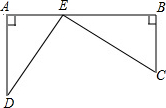 如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由.
如图,铁路上A、B两站相距25km,C,D为两村庄,且DA⊥AB,CB⊥AB,已知AD=15km,CB=10km,在AB上是否存在一点E,使它到C、D两村庄的距离相等?若存在,求出此时AE的距离;若不存在,请说明理由.
 如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36°
如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36°