题目内容
8.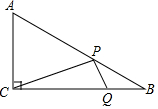 如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )| A. | 3$\sqrt{3}$ | B. | 3+$\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
分析 作C关于AB的对称点C′,过C′作C′Q⊥BC于Q,交AB于P,则C′Q=CP+PQ的最小值,解直角三角形得到AB=4$\sqrt{3}$,根据三角形的面积公式得到CC′=2×$\frac{AC•BC}{AB}$=2×$\frac{2\sqrt{3}×6}{4\sqrt{3}}$=6,根据相似三角形的性质即可得到结论.
解答  解:作C关于AB的对称点C′,过C′作C′Q⊥BC于Q,交AB于P,
解:作C关于AB的对称点C′,过C′作C′Q⊥BC于Q,交AB于P,
则C′Q=CP+PQ的最小值,
∵在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,
∴AB=4$\sqrt{3}$,
∴CC′=2×$\frac{AC•BC}{AB}$=2×$\frac{2\sqrt{3}×6}{4\sqrt{3}}$=6,
∵∠B=∠C′,∠C′QC=∠ACB=90°,
∴△CC′Q∽△BAC,
∴$\frac{CC′}{AB}=\frac{C′Q}{BC}$,即$\frac{6}{4\sqrt{3}}=\frac{C′Q}{6}$,
∴C′Q=3$\sqrt{3}$.
故选A.
点评 本题考查了线路最短的问题,确定动点P为何位置时,使PC+PM的值最小是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13. 如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
 如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )
如图,直线a∥b,直线c与直线a,b都相交,若∠1=55°,则∠2等于( )| A. | 55° | B. | 45° | C. | 35° | D. | 25° |
 如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).
如图,在直角坐标系中,第一次将△OAB交换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3…已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).观察每次变换前后的三角形有何变化,按照变换规律,第五次变换后得到的三角形A5的坐标是(32,3),B5的坐标是(64,0),An的坐标是(2n,3).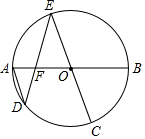 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,ED交AB于点F. 如图所示,在?ABCD中,点E,F分别在边BC和AD上,且CE=AF,
如图所示,在?ABCD中,点E,F分别在边BC和AD上,且CE=AF,