题目内容
20.(1)计算:$(\frac{1}{2})^{-1}$+|1-$\sqrt{3}$|-$\root{3}{-8}$-2sin60°;(2)已知关于x、y的方程组$\left\{\begin{array}{l}{mx-\frac{1}{2}ny=\frac{1}{2}}\\{mx+ny=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,求m、n的值.
分析 (1)原式利用负整数指数幂,绝对值的代数意义,立方根定义,以及特殊角的三角函数值计算即可得到结果;
(2)把x与y的值代入方程组解得即可求出m与n的值.
解答 解:(1)原式=2+$\sqrt{3}$-1+2-$\sqrt{3}$=3;
(2)把$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}{2m-\frac{3}{2}n=\frac{1}{2}①}\\{2m+3n=5②}\end{array}\right.$,
②-①得:$\frac{9}{2}$n=$\frac{9}{2}$,
解得:n=1,
把n=1代入②得:m=1,
∴$\left\{\begin{array}{l}{m=1}\\{n=1}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
8.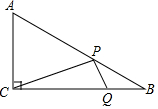 如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,BC=6,动点P,Q分别在边AB,BC上,则CP+PQ的最小值为( )| A. | 3$\sqrt{3}$ | B. | 3+$\frac{3\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
 如图,把边长为4cm的正方形ABCD先向右平移1cm再向上平移1cm得到正方形EFGH,则阴影部分的面积为9cm2.
如图,把边长为4cm的正方形ABCD先向右平移1cm再向上平移1cm得到正方形EFGH,则阴影部分的面积为9cm2. 根据下列语句画出图形.
根据下列语句画出图形.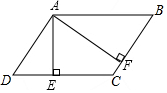 如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.
如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.