题目内容
18．计算：（1）-12+$\root{3}{64}$-（-2）×$\sqrt{9}$；
（2）|$\sqrt{2}$+2|-|1-$\sqrt{2}$|+$\sqrt{\frac{1}{4}}$．
分析 （1）原式利用乘方的意义，平方根、立方根定义计算即可得到结果；
（2）原式利用绝对值的代数意义，算术平方根定义计算即可得到结果．
解答 解：（1）原式=-1+4-（-2）×3=-1+4+6=9；
（2）原式=$\sqrt{2}$+2-$\sqrt{2}$+1+$\frac{1}{2}$=$\frac{7}{2}$．
点评 此题考查了实数的运算，绝对值，以及平方根、立方根，熟练掌握各自的性质是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．
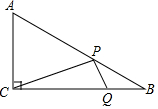如图，在Rt△ABC中，∠ACB=90°，AC=2$\sqrt{3}$，BC=6，动点P，Q分别在边AB，BC上，则CP+PQ的最小值为（ ）
如图，在Rt△ABC中，∠ACB=90°，AC=2$\sqrt{3}$，BC=6，动点P，Q分别在边AB，BC上，则CP+PQ的最小值为（ ）| A． | 3$\sqrt{3}$ | B． | 3+$\frac{3\sqrt{3}}{2}$ | C． | 2$\sqrt{3}$ | D． | 2+$\sqrt{3}$ |
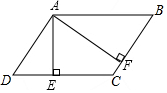如图，在平行四边形ABCD中，AE⊥CD，垂足为E，AF⊥BC，垂足为F，AD=4，BF=3，∠EAF=60°，设$\overrightarrow{AB}$=$\overrightarrow{a}$，如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$（k≠0），那么k的值是-$\frac{2}{3}$．
13．下列实数中，是无理数的为（ ）
| A． | -3.567 | B． | 0.101001 | C． | $\sqrt{2}$ | D． | $\frac{1}{3}$ |
