题目内容
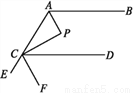
如图,AP,CP分别平分∠BAC,∠ACD,∠P=90°,设∠BAP=α.
(1)用α表示∠ACP;
(2)求证:AB∥CD;
(3)若AP∥CF,求证:FC平分∠DCE.
（1）∠CAP=90°-α； （2）证明见解析；（3）证明见解析；
【解析】试题分析：（1）由角平分线的定义可得∠PAC=α，在Rt△PAC中根据直角三角形的性质可求得∠ACP；
（2）结合（1）可求得∠ACD，可证明∠ACD+∠BAC=180°，可证明AB∥CD；
（3）由平行线的性质可得∠ECF=∠CAP，∠ECD=∠CAB，结合条件可证得∠ECF=∠FCD，可证得结论．
...
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
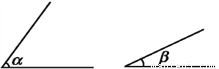
如图,已知∠α,∠β且∠α>∠β.求作∠γ,使∠γ=∠α-∠β.
见解析
【解析】【试题分析】运用基本作图“作一个角等于已知角”，作出∠α,∠β,根据两角之差即可.
【试题解析】
如图.
(1)作射线OA.
(2)以OA为一边,作∠BOA,使∠BOA=∠α.
(3)以OB为一边在∠AOB内作∠BOC,使∠BOC=∠β,则∠AOC=∠α-∠β.故∠AOC=∠γ就是所求作的角. 如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如图②所示，以下对图形M的平移方法叙述正确的是 （ ）
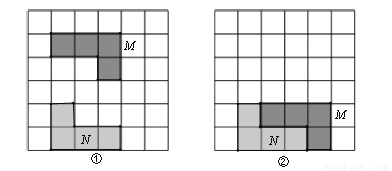
A. 向右平移2个单位，向下平移3个单位
B. 向右平移1个单位，向下平移3个单位
C. 向右平移1个单位，向下平移4个单位
D. 向右平移2个单位，向下平移4个单位
B
【解析】试题解析：根据图形M平移前后对应点的位置变化可知，图形M的平移方法为：向右平移1个单位，向下平移3个单位.
故选B. 已知sinA=0.1782，则锐角A的度数大约为（ ）
A. 8° B. 9° C. 10° D. 11°
C
【解析】试题分析：使用2nd键，然后按sin-1 0.1782即可求出∠A的度数．
∵sinA=0.1782，
∴∠A≈10°．
故选：C． 用计算器求sin50°的值，按键顺序是（ ）
A.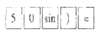 
B.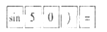 
C. 
D.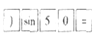 
B
【解析】试题分析：先按键“sin”，再输入角的度数50°，按键“=”即可得到结果．
故选B． 若2x=3,2y=5,求42x+y的值.
2025
【解析】试题分析：逆用幂的运算法则解答即可．
试题解析：【解析】
因为2x=3，2y=5，所以42x+y=42x×4y=24x×22y=（2x）4×（2y）2=34×52=2 025． 如图是有若干个全等的等边三角形拼成的纸板，若某人向纸板上投掷飞镖，（每次飞镖均落在纸板上），则飞镖落在阴影部分的概率是_____．
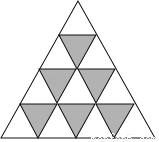
【解析】如图：阴影部分的面积占6份，总面积是16份，
∴飞镖落在阴影部分的概率是=，
故答案为： ． 若不等式(a－3)x＞1的解集为x＜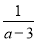
，则a的取值范围是_____.
a＜3
【解析】∵(a?3)x>1的解集为x<，
∴不等式两边同时除以(a?3)时不等号的方向改变，
∴a?3<0，
∴a<3.
故答案为：a<3. 如图，△ACB和△DCE均为等腰三角形，点A、D、E在同一直线上，连接BF.若∠CAB＝∠CBA＝∠CDE＝∠CED＝50°.
(1)求证：AD＝BE；
(2)求∠AEB的度数．
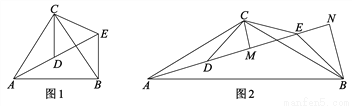
(1)见解析；（2）80°.
【解析】试题分析：（1）通过角的计算找出∠ACD=∠BCE，再结合△ACB和△DCE均为等腰三角形可得出“AC=BC，DC=EC”，利用全等三角形的判定（SAS）即可证出△ACD≌△BCE，由此即可得出结论AD=BE；
（2）结合（1）中的△ACD≌△BCE可得出∠ADC=∠BEC，再通过角的计算即可算出∠AEB的度数．
试题解析：（1）∵∠CAB＝...