题目内容
如图，直线AB与CD相交于点O，∠AOD=50°，则∠BOC=__________．
50
【解析】根据对顶角相等，易得∠BOC=50°
练习册系列答案
名校课堂系列答案
相关题目
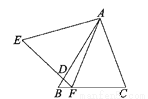
如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D.给出下列结论：①∠EAB=∠FAC；②AF=AC；③∠C=∠EFA；④AD=AC.其中正确的结论是_____(填序号)．
①②③
【解析】【解析】
在△AEF和△ABC中，∵AB=AE，∠B=∠E，BC=EF，∴△AEF≌△ABC（SAS），∴∠EAF=∠BAC，AF=AC，∠C=∠EFA，∴∠EAB=∠FAC，故①②③正确，④错误；
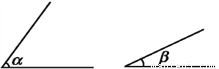
所以答案为：①②③． 如图,已知∠α,∠β且∠α>∠β.求作∠γ,使∠γ=∠α-∠β.
见解析
【解析】【试题分析】运用基本作图“作一个角等于已知角”，作出∠α,∠β,根据两角之差即可.
【试题解析】
如图.
(1)作射线OA.
(2)以OA为一边,作∠BOA,使∠BOA=∠α.
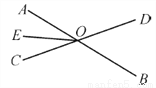
(3)以OB为一边在∠AOB内作∠BOC,使∠BOC=∠β,则∠AOC=∠α-∠β.故∠AOC=∠γ就是所求作的角. 如图所示，直线AB，CD相交于点O，OE平分∠AOC，若∠AOD-∠DOB=60°，则∠EOB=__________.
150°
【解析】∵∠AOD－∠BOD＝60°,
∴∠AOD=∠BOD+60°,
∵AB为直线,∴∠AOD+∠BOD=∠AOB=180°,
∴∠BOD+60°+∠BOD=180°,
∴∠BOD=60°,
∵∠AOC与∠BOD为对顶角,
∴∠AOC＝∠BOD=60°,
∵OE平分∠AOC,
∴∠AOE＝∠AOC=30°,
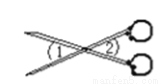
∴∠BOE=180... 如图是一把剪刀，其中∠1=40°，则∠2= 度，其理由是 。
40°、对顶角相等.
【解析】
试题分析：根据图示可得∠1和∠2为对顶角，根据对顶角的性质求出角的度数. 如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路，宽均为1米，其它部分均种植花草．试求出种植花草的面积是多少？
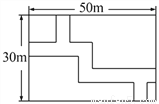
1421m2
【解析】试题分析：将横向的小路平移至长方形的上边，将纵向小路平移至长方形的左边，则剩余部分即为种植花草的面积．
【解析】
将横向的小路平移至长方形的上边，将纵向小路平移至长方形的左边，如图所示：
所以种植花草的面积＝(50－1)(30－1)＝1421m2． 如图，在6×6方格中有两个涂有阴影的图形M、N，①中的图形M平移后位置如图②所示，以下对图形M的平移方法叙述正确的是 （ ）
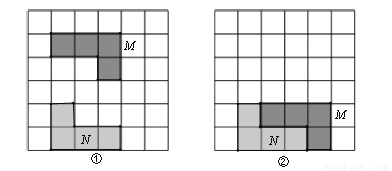
A. 向右平移2个单位，向下平移3个单位
B. 向右平移1个单位，向下平移3个单位
C. 向右平移1个单位，向下平移4个单位
D. 向右平移2个单位，向下平移4个单位
B
【解析】试题解析：根据图形M平移前后对应点的位置变化可知，图形M的平移方法为：向右平移1个单位，向下平移3个单位.
故选B. 已知sinA=0.1782，则锐角A的度数大约为（ ）
A. 8° B. 9° C. 10° D. 11°
C
【解析】试题分析：使用2nd键，然后按sin-1 0.1782即可求出∠A的度数．
∵sinA=0.1782，
∴∠A≈10°．
故选：C． 若不等式(a－3)x＞1的解集为x＜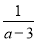
，则a的取值范围是_____.
a＜3
【解析】∵(a?3)x>1的解集为x<，
∴不等式两边同时除以(a?3)时不等号的方向改变，
∴a?3<0，
∴a<3.
故答案为：a<3.