题目内容
 阅读理解:对于任意正实数a、b,
阅读理解:对于任意正实数a、b,∵(
| a |
| b |
| ab |
| ab |
| ab |
根据上述内容,回答下列问题:
(1)若m>0,只有当m=
| 1 |
| m |
(2)探索应用:已知,点Q(-3,-4)是反比例函数图象y=
| k |
| x |
| k |
| x |
(3)已知x>0,则自变量x为何值时,函数y=
| x |
| x2-2x+25 |
考点:反比例函数综合题
专题:代数几何综合题
分析:(1)根据已知条件,当m=
时,m+
有最小值2
,进而求出即可;
(2)连接PO,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,首先利用S四边形AQBP=S四边形AQBO+S△AOP+S△BOP,再结合当2x=
,时SAQBP的面积最小,求出x的值,进而得出答案;
(3)首先设y′=
=x-2+
,当x=
时y'最小,进而得出x的值以及y的值.
| 1 |
| m |
| 1 |
| m |
m×
|
(2)连接PO,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,首先利用S四边形AQBP=S四边形AQBO+S△AOP+S△BOP,再结合当2x=
| 18 |
| x |
(3)首先设y′=
| x2-2x+25 |
| x |
| 25 |
| x |
| 25 |
| x |
解答: 解:(1)当m=
解:(1)当m=
时,则m2=1,
解得m=±1,
∵m>0,
∴m=1,
∴m+
有最小值是2;
故答案为:1,2;
(2)由题意得,SAQBO=3×4=12,反比例函数解析式为:y=
,
连接PO,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,设点P的坐标为(x,
),
∴S△AOP=
×AO×PM=
×3×
=
,
S△BOP=
×BO×PN=
×4×x=2x,
S四边形AQBP=S四边形AQBO+S△AOP+S△BOP=2x+
+12,
当2x=
,时SAQBP的面积最小,解得x1=3,x2=-3(舍去),
∴当x=3时,S四边形AQBP=2×3+
+12=24,
∴四边形AQBP面积的最小值为24;
(3)设y′=
=x-2+
,
当x=
时y'最小,∴当x=5时,y'最小=8,
∴当x=5时,y最大=
.
 解:(1)当m=
解:(1)当m=| 1 |
| m |
解得m=±1,
∵m>0,
∴m=1,
∴m+
| 1 |
| m |
故答案为:1,2;
(2)由题意得,SAQBO=3×4=12,反比例函数解析式为:y=
| 12 |
| x |
连接PO,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,设点P的坐标为(x,
| 12 |
| x |
∴S△AOP=
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| x |
| 18 |
| x |
S△BOP=
| 1 |
| 2 |
| 1 |
| 2 |
S四边形AQBP=S四边形AQBO+S△AOP+S△BOP=2x+
| 18 |
| x |
当2x=
| 18 |
| x |
∴当x=3时,S四边形AQBP=2×3+
| 18 |
| 3 |
∴四边形AQBP面积的最小值为24;
(3)设y′=
| x2-2x+25 |
| x |
| 25 |
| x |
当x=
| 25 |
| x |
∴当x=5时,y最大=
| 1 |
| 8 |
点评:此题主要考查了反比例函数综合以及四边形面积公式和函数最值求法等知识,利用已知得出当2x=
,时SAQBP的面积最小进而得出x的值是解题关键.
| 18 |
| x |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
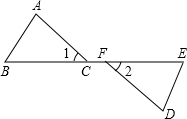 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是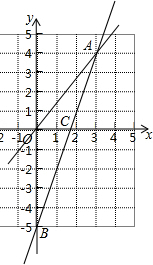 如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C.
如图,一个正比例函数y1=k1x的图象与一个一次函数y2=k2x+b的图象相交于点A(3,4),且一次函数y2的图象与y轴相交于点B(0,-5),与x轴交于点C. 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB 于点E,且ME=3,AM=6,AE=3
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB 于点E,且ME=3,AM=6,AE=3