题目内容
6．若抛物线y=3x2+（m2-2m-15）x-4的顶点在y轴上，则m的值是5或-3．分析 根据y=ax2+bx+c的顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），可得答案．
解答 解：抛物线y=3x2+（m2-2m-15）x-4的顶点在y轴上，得
-$\frac{{m}^{2}-2m-15}{2×3}$=0，
即m2-2m-15=0，
解得m=5或m=-3．
故答案为：5或-3．
点评 本题考查了二次函数的性质，利用了y=ax2+bx+c的顶点坐标是（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$），当a＞0时，在对称轴左侧y随x的增大而减小，在对称轴右侧y随x的增大而增大；当a＜0时，在对称轴左侧y随x的增大而增大，在对称轴右侧y随x的增大而减小．
练习册系列答案
相关题目
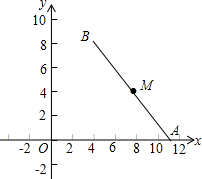如图，线段AB在平面直角坐标系中，A（11，0），B（5，8）．点M为线段AB上一点，M（8，4）．将线段AB向左平移，使点B的对应点C落在y轴上．点A的对应点为D．