题目内容
1.计算(两种方法思维):(1)49(m+n)2-(3m-n)2(2)(m+n)2(m-n)2解:(1)方法1、直接利用乘法公式计算;方法2、逆用乘法公式计算;
解:(2)方法1、直接利用乘法公式计算;方法2、运用幂的运算性质计算.
分析 (1)利用完全平方公式、平方差公式,即可解答;
(2)利用完全平方公式、平方差公式,即可解答;
解答 解:(1)方法1:49(m+n)2-(3m-n)2
=49(m2+2mn+n2)-(9m2-6mn+n2)
=49m2+98mn+49n2-9m2+6mn-n2
=40m2+104mn+48n2.
方法2:49(m+n)2-(3m-n)2
=[7(m+n)+(3m-n)][7(m+n)-(3m-n)]
=(10m+6n)(4m+8n)
=40m2+104mn+48n2.
(2)方法1、(m+n)2(m-n)2
=(m2+2mn+n+n2)(m2-2mn+n2)
=m4-2m2n2+n4.
方法2、(m+n)2(m-n)2
=[(m+n)(m-n)]2
=(m2-n2)2
=m4-2m2n2+n4.
点评 本题考查了完全平方公式、平方差公式,解决本题的关键是熟记公式.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.用下列图形不能进行平面镶嵌的是( )
| A. | 正三角形和正四边形 | B. | 正三角形和正六边形 | ||
| C. | 正四边形和正八边形 | D. | 正四边形和正十二边形 |
12.若关于x的方程3kx2+12x+k+1=0有两个相等的实根,则k的值为( )
| A. | -4 | B. | 3 | C. | -4或3 | D. | $\frac{1}{2}$或-$\frac{2}{3}$ |
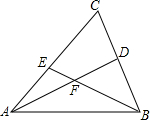 如图所示,在△ABC中,AD是BC边的中线,F是AD的中点,连接BF并延长交AC于E,求证:EC=2AE.
如图所示,在△ABC中,AD是BC边的中线,F是AD的中点,连接BF并延长交AC于E,求证:EC=2AE. 如图,在长方形ABCD,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设F、Q两点移动t秒(0<t<5)后.
如图,在长方形ABCD,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB向点B移动,设F、Q两点移动t秒(0<t<5)后.