题目内容
11.若b+$\frac{1}{b}$=9,求2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$的值为2$\sqrt{11}$.分析 先求(2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$)2值,利用完全平方公式得到(2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$)2=4b+8+$\frac{4}{b}$=8+4(b+$\frac{1}{b}$),再利用整体代入的方法计算,然后根据算术平方根的定义求解.
解答 解:因为b+$\frac{1}{b}$=9,
所以(2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$)2=4b+8+$\frac{4}{b}$=8+4(b+$\frac{1}{b}$)=8+4×9=44,
而2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$>0,
所以2$\sqrt{b}$+2$\frac{1}{\sqrt{b}}$=$\sqrt{44}$=2$\sqrt{11}$.
故答案为2$\sqrt{11}$.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列各组线段能构成直角三角形的一组是( )
| A. | 5cm,9cm,12cm | B. | 7cm,12cm,13cm | C. | 30cm,40cm,50cm | D. | 3cm,4cm,6cm |
 为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=25m,DC=30m,DE=30m,那么你能算出池塘的宽AB吗?
为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使DE⊥AC,测出AD=25m,DC=30m,DE=30m,那么你能算出池塘的宽AB吗?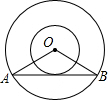 如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.
如图,⊙O的半径为8cm,圆内的弦AB=8$\sqrt{3}cm$,以点O为圆心,4cm为半径作小圆,求证:直线AB与小圆相切.