题目内容
6.若(m-3)2与(n+$\frac{1}{2}$)2互为相反数,则nm=-$\frac{1}{8}$.分析 根据非负数的性质列式求出m、n的值,然后代入代数式进行计算即可得解.
解答 解:∵(m-3)2与(n+$\frac{1}{2}$)2互为相反数,
∴(m-3)2+(n+$\frac{1}{2}$)2=0,
∴m-3=0,n+$\frac{1}{2}$=0,
解得m=3,n=-$\frac{1}{2}$,
∴nm=-$\frac{1}{8}$
故答案为:-$\frac{1}{8}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
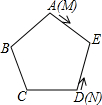 如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.
如图,M、N是正五边形ABCDE各边上的两个动点,若它们分别从顶点A、D出发,同时沿正五方形的边移动,M点以顺时针方向移动,N点以逆时针方向移动,假设点M的速度是点N的速度的5倍,则它们第2014次相遇在( )边上.