题目内容
已知⊙O的内接正六边形的边长为2,求⊙O的外切正三角形的边长.
考点:正多边形和圆
专题:
分析:根据⊙O的内接正六边形的边长为2,可得出⊙O的半径为2,⊙O的半径、⊙O外切正三角形的半径、正三角形的边长的一半组成直角三角形,根据30°的锐角所对的直角边等于斜边的一半求解即可.
解答: 解:如图,
解:如图,
∵⊙O的内接正六边形的边长为2,
∴OC=2,
∵∠OAC=30°,
∴OA=4,
∴AC=
=
=2
,
∴AB=2AC=4
.
 解:如图,
解:如图,∵⊙O的内接正六边形的边长为2,
∴OC=2,
∵∠OAC=30°,
∴OA=4,
∴AC=
| OA2-OC2 |
| 42-22 |
| 3 |
∴AB=2AC=4
| 3 |
点评:本题考查了正多边形与圆的知识.注意圆内接正六边形的边长和圆的半径相等.

练习册系列答案
相关题目
 如图,已知△ABC是等边三角形,则∠BDC=( )
如图,已知△ABC是等边三角形,则∠BDC=( )| A、30° | B、60° |
| C、90° | D、120° |
 如图,正五边形ABCDE的对角线为BE,则∠ABE的度数为
如图,正五边形ABCDE的对角线为BE,则∠ABE的度数为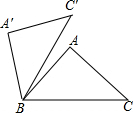 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕点B逆时针旋转一定角度,点C′恰落在边BC上的高所在的直线上,则边BC在旋转过程中所扫过的面积为( )