题目内容
14.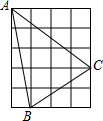 如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )
如图,在正方形网格中,每个小正方形的边长为1,则网格上的△ABC,其边长是无理数的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据勾股定理求出△ABC各边的长,再由无理数的定义即可得出结论.
解答 解:∵AB=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,$\sqrt{26}$是无理数;
AC=$\sqrt{{4}^{2}+{3}^{2}}$=5,5是有理数;
BC=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,$\sqrt{13}$是无理数,
∴边长是无理数的有2个.
故选C.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
5.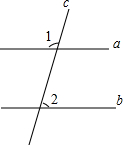 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )| A. | 108° | B. | 82° | C. | 72° | D. | 62° |
2.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
6.某小学组织六年级学生到郊外春游.如果每辆汽车坐40人,则有5人没有上车;如果每辆汽车坐48人,则空出一辆汽车,并且其中有一辆车还可以再坐11人.现假设共有x个学生,y辆汽车,则可列出的方程组为( )
| A. | $\left\{\begin{array}{l}{40x+5=y}\\{48x-59=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{40y+5=x}\\{48(y-1)=x-11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{40y+5=x}\\{48y-11=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{40y=x-5}\\{48(y-1)=x+11}\end{array}\right.$ |
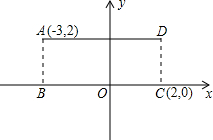
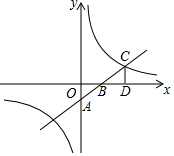 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{n}{x}$的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=$\frac{n}{x}$的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.