题目内容
3.将函数y=2x+3的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+3|的图象,若函数y=|2x+3|的图象在直线y=-$\frac{1}{4}$x+b下方的点的横坐标x满足-3<x<-1,则b的取值范围是-$\frac{9}{4}$<b<-$\frac{3}{4}$.分析 根据翻折的性质,可得分段函数,根据自变量与函数值得对应关系,可得交点坐标,根据待定系数法,可得答案.
解答 解:由题意,得
函数解析式为y=$\left\{\begin{array}{l}{2x+3(x≥-\frac{3}{2})}\\{-2x-3(x<-\frac{3}{2})}\end{array}\right.$,
当x=-3时,y=-3,即点的坐标(-3,-3)
将(-3,-3)代入函数解析式,得
-3=-$\frac{1}{4}$×(-3)+b,
解得b=-$\frac{9}{4}$;
当x=-1时,y=-1,即点的坐标(-1,-1),
将点的坐标代入函数解析式,得
-1=-$\frac{1}{4}$×(-1)+b,
解得b=-$\frac{3}{4}$,
若函数y=|2x+3|的图象在直线y=-$\frac{1}{4}$x+b下方的点的横坐标x满足-3<x<-1,则b的取值范围是-$\frac{9}{4}$<b<-$\frac{3}{4}$,
故答案为:-$\frac{9}{4}$<b<-$\frac{3}{4}$.
点评 本题考查了一次函数图象与几何变换,利用翻折得出分段函数是解题关键,又利用了自变量与函数值的对应关系,待定系数法.

练习册系列答案
相关题目
5.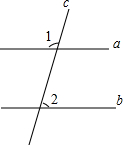 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )| A. | 108° | B. | 82° | C. | 72° | D. | 62° |
6.某小学组织六年级学生到郊外春游.如果每辆汽车坐40人,则有5人没有上车;如果每辆汽车坐48人,则空出一辆汽车,并且其中有一辆车还可以再坐11人.现假设共有x个学生,y辆汽车,则可列出的方程组为( )
| A. | $\left\{\begin{array}{l}{40x+5=y}\\{48x-59=y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{40y+5=x}\\{48(y-1)=x-11}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{40y+5=x}\\{48y-11=x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{40y=x-5}\\{48(y-1)=x+11}\end{array}\right.$ |
10.据统计,2016年长春市接待旅游人数约67000000人次,67000000这个数用科学记数法表示为( )
| A. | 67×106 | B. | 6.7×105 | C. | 6.7×107 | D. | 6.7×108 |
 如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.
如图,△ABC中,∠A=50°,∠B=70°,CD平分∠ACB,DE交AB于D交AC于E,∠CDE=30°,求∠ADE的度数.