题目内容
1. 记抛物线y=-x2+100的图象与y轴正半轴的交点为A,将线段OA分成100等份,设分点分别为P1,P2,…,P99,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,Q99,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就记W=S12+S22+S32+…+S992,W的值为( )
记抛物线y=-x2+100的图象与y轴正半轴的交点为A,将线段OA分成100等份,设分点分别为P1,P2,…,P99,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…,Q99,再记直角三角形OP1Q1,P1P2Q2,…的面积分别为S1,S2,…,这样就记W=S12+S22+S32+…+S992,W的值为( )| A. | 1237 | B. | 1238 | C. | 1237.5 | D. | 1238.5 |
分析 根据等分求出OP1=P1P2=P2P3=P3P4=…=P98P99=1,再利用抛物线解析式求出P1Q1,P2Q2,…,P99Q99的平方的值,利用三角形的面积表示出S1,S2,…,平方后相加,然后根据等差数列求和公式进行计算即可得解.
解答 解:∵P1,P2,…,P99将线段OA分成100等份,
∴OP1=P1P2=P2P3=P3P4=…=P98P99=1,
∵过分点P1作y轴的垂线,与抛物线交于点Q1,
∴-x2+100=1,
解得x2=99,
∴S12=($\frac{1}{2}$×1×P1Q1)2=$\frac{1}{4}$×99,
同理可得S22=$\frac{1}{4}$×98,
S32=$\frac{1}{4}$×97,
…
S992=$\frac{1}{4}$×1,
∴w=S12+S22+S32+…+S992
=$\frac{1}{4}$×99+$\frac{1}{4}$×98+$\frac{1}{4}$×98+…+$\frac{1}{4}$×1
=$\frac{1}{4}$×$\frac{99×(99+1)}{2}$=1237.5,
故选C.
点评 本题是对二次函数的综合考查,根据图形的变化规律,分别表示出各三角形的面积的平方是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)
如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)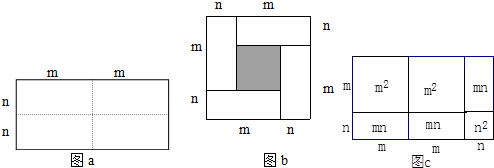
 如图是一个水平放置的油管的截面图,其中油面的宽AB为16cm,油面的深度CD=4cm,求油管截面圆的半径.
如图是一个水平放置的油管的截面图,其中油面的宽AB为16cm,油面的深度CD=4cm,求油管截面圆的半径.