题目内容
7.平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(点B在点A左侧),与y轴交于点C,点A、C的坐标分别为(3,0),(0,3),对称轴直线x=1交x轴于点E,点D为顶点.(1)求抛物线的解析式;
(2)点P是直线AC下方的抛物线上一点,且S△PAC=2S△DAC,求点P的坐标;
(3)点M是第二象限内抛物线上一点,且∠MAC=∠ADE,求点M的坐标.
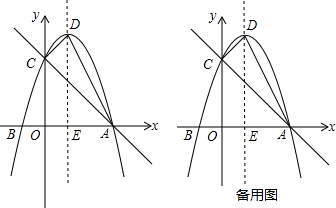
分析 (1)由已知中点A、C的坐标分别为(3,0),(0,3),对称轴为直线x=1,得出B点坐标,进而利用交点式求出即可求出抛物线的解析式;
(2)由已知中C点坐标,再假设出P点坐标,可求出直线PC解析式,求出R点坐标,进而根据S△PAC=2S△DAC,可得点P的坐标;
(3)过点C作CH⊥DE交DE于点H,设AC交对称轴于点G,AM交y轴于点N,由∠MAC=∠ADE,可得N点坐标,进而求出AN的方程,联立直线与抛物线方程可得M点坐标.
解答 解:(1)由对称轴x=1,A(3,0),可得B点坐标(-1,0)
设y=a(x-3)(x+1),把C(0,3)代入得,3=-3a,
解得:a=-1,
所求解析式为:y=-x2+2x+3;
(2)如图:y=-x2+2x+3=-(x-1)2+4,顶点D(1,4),
由A(3,0)、C(0,3),得直线AC解析式为y=-x+3;
设对称轴交AC于点G,则G(1,2),
∴S△DAC=$\frac{1}{2}$(4-2)×3=3,
设P点(m,-m2+2m+3),
设PC解析式为:y=qx+p,
∴$\left\{\begin{array}{l}{P=3}\\{mk+3=-{m}^{2}+2m+3}\end{array}\right.$,
解得:k=-m-2,
∴PC解析式为:y=(-m+2)x+3,
设PC与x轴交于点R,
∴R($\frac{3}{m-2}$,0),
∴AR=3-$\frac{3}{m-2}$,
∴S△APR+S△CAR=$\frac{1}{2}$(3-$\frac{3}{m-2}$)×(m2-2m-3)+$\frac{1}{2}$×(3-$\frac{3}{m-2}$)×3=$\frac{3{m}^{2}}{2}$-$\frac{9m}{2}$,
则S△PAC=$\frac{3{m}^{2}}{2}$-$\frac{9m}{2}$,
由S△PAC=2S△DAC,
∴$\frac{3{m}^{2}}{2}$-$\frac{9m}{2}$=2×3,
解得:m1=4,m2=-1,把m1=4,m2=-1分别代入y=-x2+2x+3中,
∴y1=-5,y2=0,
∴P点坐标为(4,-5)或(1,0);
(3)由以上可得出:D(1,4),C(0,3),E(1,0),
如备用图:过点C作CH⊥DE交DE于点H,
∴H(-1,3),CH=DH=1,∠DCH=∠HCA=∠CA0=45°,
∴CD=$\sqrt{2}$,AC=3$\sqrt{2}$,△ACD为直角三角形,且tan∠DAC=$\frac{1}{3}$.
设AC交对称轴于点G,AM交y轴于点N,
∵∠DAC+∠ADE=∠DGC=45°,∠CAM+∠MAO=∠CAO=45°,∠ADE=∠CAM,∠DAC=∠MAO,
∴tan∠MAO=$\frac{1}{3}$.
∵A(3,0),
∴ON=1,即N(0,1),
设直线AN解析式为:y=dx+h
∴$\left\{\begin{array}{l}{h=1}\\{3d+h=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{h=1}\\{d=-\frac{1}{3}}\end{array}\right.$,
∴直线AN解析式为y=-$\frac{1}{3}$x+1,
联立方程$\left\{\begin{array}{l}{y=-\frac{1}{3}x+1}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
得:x=3(舍)或x=-$\frac{2}{3}$,
∴点M的坐标为(-$\frac{2}{3}$,$\frac{11}{9}$).
点评 本题考查的知识点是函数解析式的求法,二次函数的图象和性质,是二次函数与解析几何知识的综合应用,难度较大.

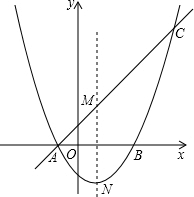 如图,抛物线y=$\frac{1}{2}$x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
如图,抛物线y=$\frac{1}{2}$x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称. 已知如图,AC、BD相交于点O,且被点O互相平分,求证:
已知如图,AC、BD相交于点O,且被点O互相平分,求证: 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F. 如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2),点B的坐标为(-4,5),点C的坐标为(-5,3).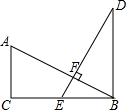 如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.
如图,已知AC⊥CB,DB⊥CB,AB⊥DE,垂足为F,AB=DE,E是BC的中点.