题目内容
19. 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.(1)求证:BE=CF;
(2)若∠BAC=60°,BE=1,求AC.
分析 (1)首先由角平分线的性质可得DE=DF,根据BD=CD,推出Rt△BED≌Rt△DFC(HL),根据全等三角形的性质得到结论;
(2)根据全等三角形的性质得到∠B=∠C,推出△ABC是等边三角形,根据等边三角形的性质得到AB=AC=BC,∠B=∠C=60°,由三角形的内角和得到∠BDE=30°,即可得到结论.
解答 (1)证明:∵AD是△ABC的角平分线,DE⊥AB、DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△DFC中,
$\left\{\begin{array}{l}{BD=CD}\\{DE=DF}\end{array}\right.$,
∴Rt△BED≌Rt△CFD(HL),
∴EB=FC;
(2)∵Rt△BED≌Rt△CFD,
∴∠B=∠C,
∴AB=AC,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=60°,
∴∠BDE=30°,
∴BD=2BE=2,
∴AC=BC=4.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质和判定,直角三角形的性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
18.去年四月份中国汽车销售总量为1530000辆,则1530000用科学记数法表示为( )
| A. | 153×104 | B. | 0.153×107 | C. | 1.53×106 | D. | 1.53×107 |
8. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )
如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为( )| A. | 70° | B. | 90° | C. | 110° | D. | 120° |
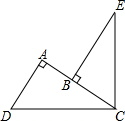 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.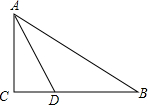 已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.
已知,在△ABC中,AD是角平分线,AD=BD,AB=2AC,求证:△ACB是直角三角形.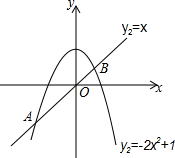 如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.
如图,抛物线y1=-2x2+1和直线y2=x交于A、B两点.