题目内容
11.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,种植草莓不超过20亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1500m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数、反比例函数或二次函数中的一种).| x(亩) | 20 | 25 | 30 | 35 |
| z(元) | 1700 | 1600 | 1500 | 1400 |
分析 (1)根据图表的性质,可以得出P关于x的函数关系式和出x的取值范围.
(2)根据利润=亩数×每亩利润,可得①当0<x≤15时 ②当15<x<20时,利润的函数式,即可解题;
解答 解:(1)观察图表的数量关系,可以得出P关于x的函数关系式为:P=$\left\{\begin{array}{l}{1800x(0<x≤15)}\\{-20x^2+2100x(x>15)}\end{array}\right.$
(2)∵利润=亩数×每亩利润,
∴①当0<x≤15时,W=1800x+1380(40-x)+2400=420x+57600;
当x=15时,W有最大值,W最大=6300+57600=63900;
②当15<x<20,W=-20x2+2100x+1380(40-x)+2400=-20(x-18)2+64080;
∴x=18时有最大值为:64080元.
综上x=18时,有最大利润64080.
点评 本题主要考查了一次函数的实际应用,解题的关键是分析题意,找到关键描述语,求出函数的解析式,用到的知识点是一次函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 下列四个物体的俯视图与给出视图一致的是( )
下列四个物体的俯视图与给出视图一致的是( )
 下列四个物体的俯视图与给出视图一致的是( )
下列四个物体的俯视图与给出视图一致的是( )| A. | 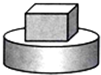 | B. | 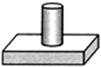 | C. | 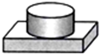 | D. | 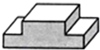 |
 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.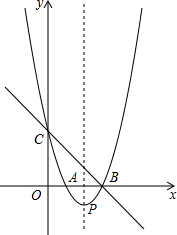 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.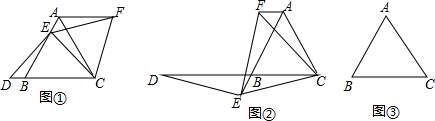
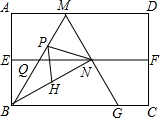 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论: